智能优化模型与算法实现

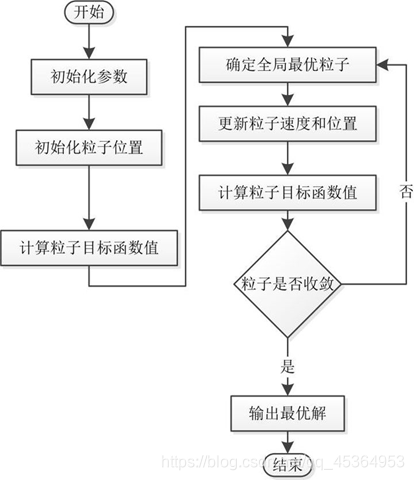
选择操作：从旧个体中以一定概率选择优良个体组成新的种群，以繁殖得到下一代。
轮盘赌法：即基于适应度比例的选择策略，个体i被选中的概率为

交叉操作：从种群中随机选择两个个体，通过两个染色体的交换组合，把父串的优秀特征遗传给子串，从而产生新的优秀个体。
采用实数交叉，第k个染色体ak和第l个染色体al在j位的交叉操作方法为,b为[0, 1]随机数：

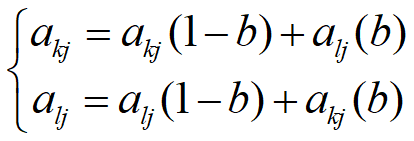
变异操作：从种群中随机选择一个个体，选择个体中的一点进行变异以产生更优秀的个体。
第i个个体的第j个基因aij进行变异操作的方法为,r为[0,1]随机数,gen为当前迭代次数，genmax为最大迭代次数：


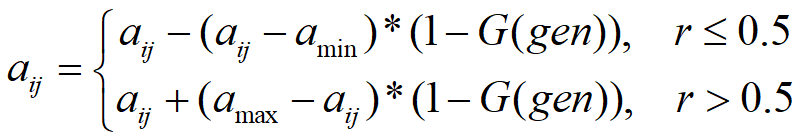
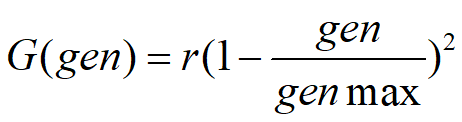
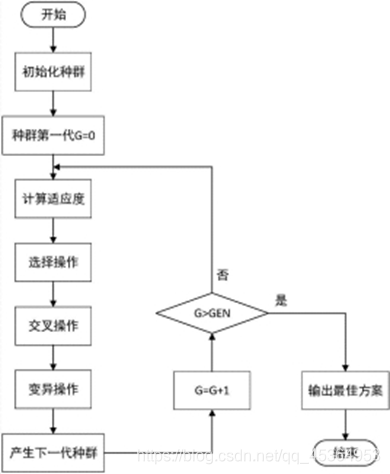
遗传算法代码很多，并且运算速度慢，相比于下面的粒子群算法更复杂，所以如果遇到优化问题，粒子群算法更方便。

核心在于更新粒子速度和位置
算法流程：

由n只鸟组成的种群$B=(B_1,B_2,B_3,\dots ,B_n)$，其中第$i$只鸟$Bi$的位置可表示为$X_i=[x_{i1},x_{i2},\dots ,x_{id}]$;其速度为$Vi=[v_{i1},v_{i2},\dots ,V_{id}]$，则第$t+1$次迭代中鸟类的位置与速度可更新为：

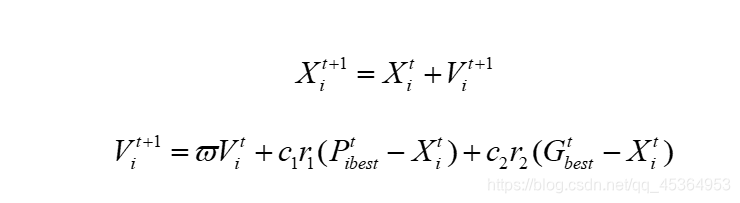
新速度= 惯性项（w V）+个体自信度（i best）+全局最优（best）

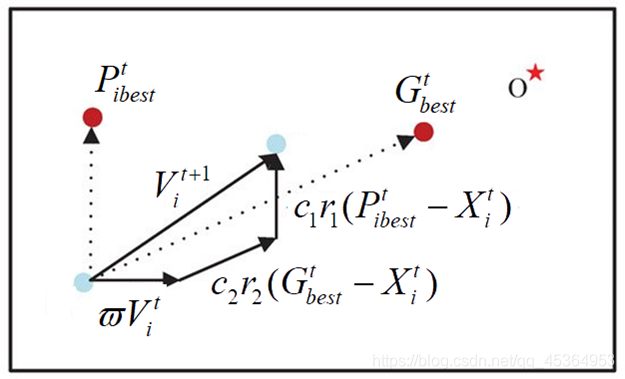
W 一般是1或者0.98，也可以随着鸟的飞行不断变小
c1 = c2 = 2或者0.5

fun函数：

粒子群算法：

惩罚函数：用于解决约束条件下的最优化问题。通过惩罚函数可以将有约束的目标函数转化为无约束的目标函数。
$f(X{)}^{{}^{\prime }}=f(X)+C$

在实际问题中大都具有多个目标且需要同时满足，即在同一问题模型中同时存在几个非线性目标，而这些目标函数需要同时进行优化处理，并且这些目标又往往是互相冲突的，称这类问题称为多目标规划问题。

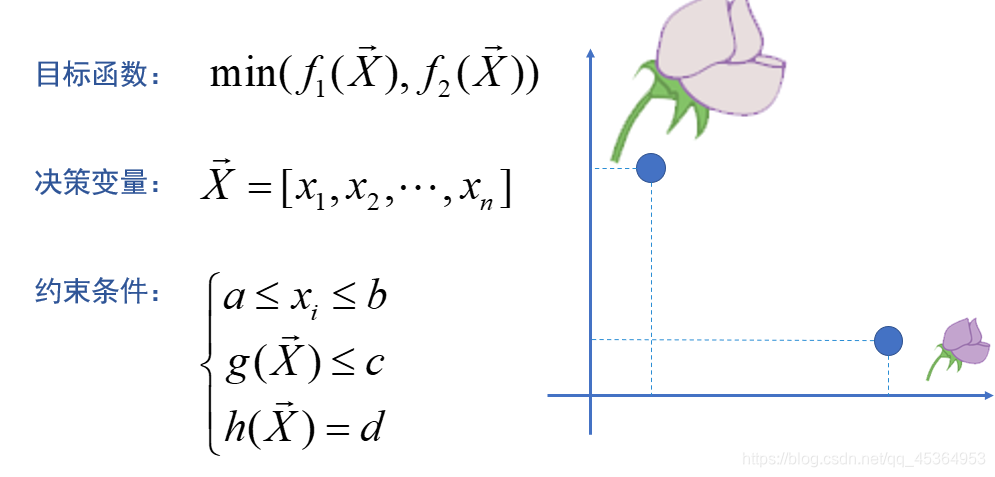
支配：
在多目标优化问题中，如果个体p至少有一个目标比个体q好，而且个体p的所有目标都不比个体q差，那么称个体p支配个体q。

A和B支配C，但是A和B不存在支配关系

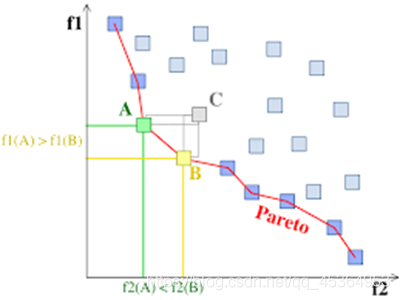
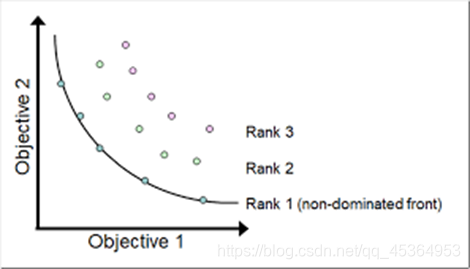
序值：如果p支配q，那么p的序值比q低。如果p和q互不支配，那么p和q有相同的序值。

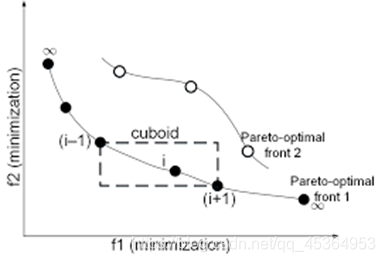
拥挤距离：用来计算某前端中的某个体与该前端中其他个体之间的距离，用以表征个体间的拥挤程度。

代码

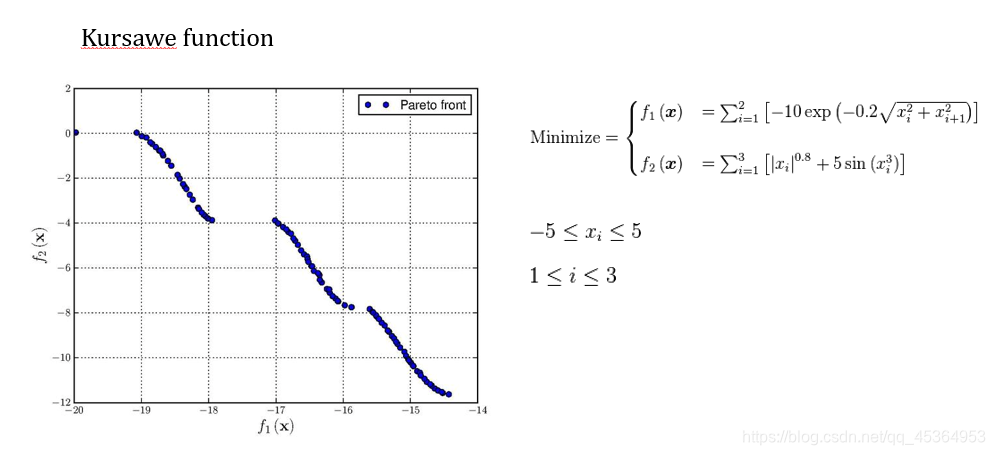
example.m

MOPSO.m