现代优化算法三部曲 ｜ 模拟退火算法

这一篇文章较为详细地介绍了模拟退火算法，但是一没有涉及代码，二没有举例，三没有深入探讨改进模型，四没有联系其他算法。

不过我比较佛，知错不改，先这样吧。

模拟退火算法来源于固体退火原理，是一种基于概率的算法。模拟退火算法是通过赋予搜索过程一种时变且最终趋于零的概率突跳性，从而可有效避免陷入局部极小并最终趋于全局最优的串行结构的优化算法。

将固体加温至充分高，再让其徐徐冷却（退火），加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小。

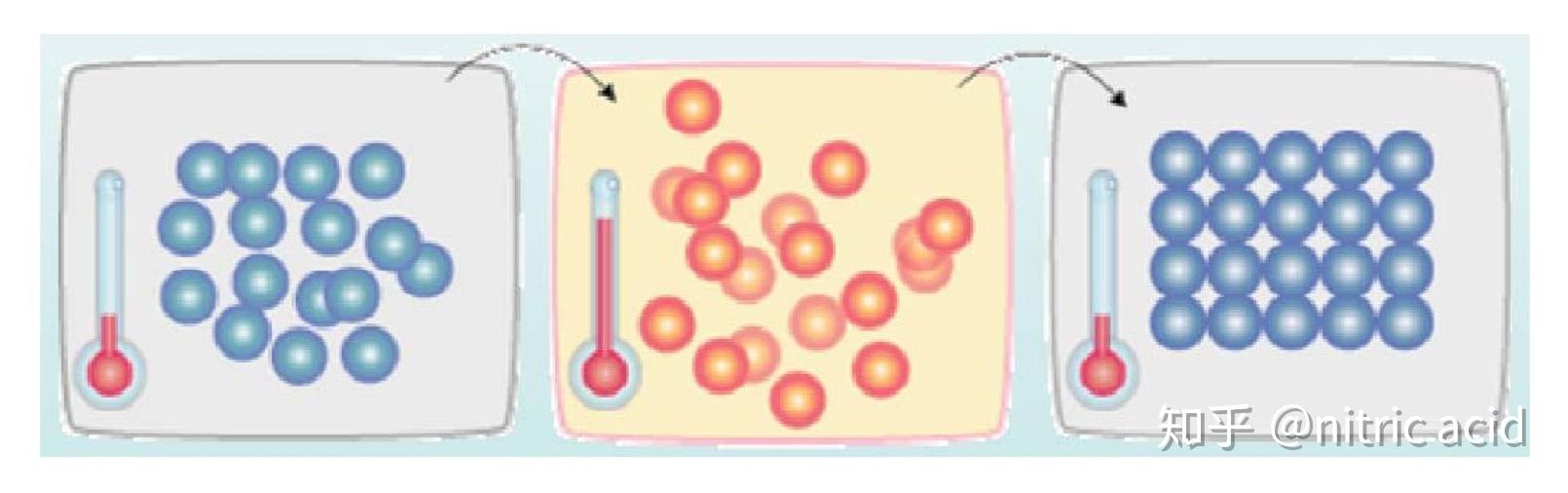
物理中，淬火（快速降温），会导致不是最低能态的非晶形；退火，可达到最低能量状态。模仿自然界退火现象而得，利用了物理中固体物质的退火过程与一般优化问题的相似性。

模拟退火算法从某一较高初温出发，伴随温度参数的不断下降,结合概率突跳特性在解空间中随机寻找目标函数的全局最优解，即在局部最优解能概率性地跳出并最终趋于全局最优。模拟退火算法是一种通用的优化算法，理论上算法具有概率的全局优化性能。

注：这里应该了解什么是局部最优解和全局最优解，还有普通贪心算法，见https://blog.csdn.net/effective_coder/article/details/8736718。

模拟退火算法包含两个部分即Metropolis算法和退火过程。Metropolis算法就是如何在局部最优解的情况下让其跳出来，是退火的基础。1953年Metropolis提出重要性采样方法，即以概率来接受新状态，而不是使用完全确定的规则，称为Metropolis准则，计算量较低。

在温度为T时，接受能量从E(Xold)到E(Xnew)的概率为P:

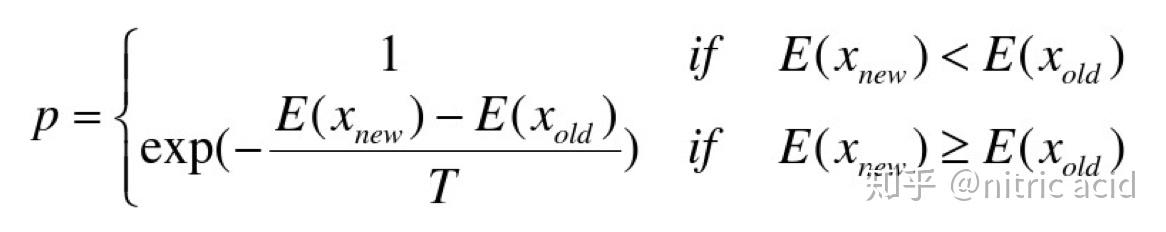
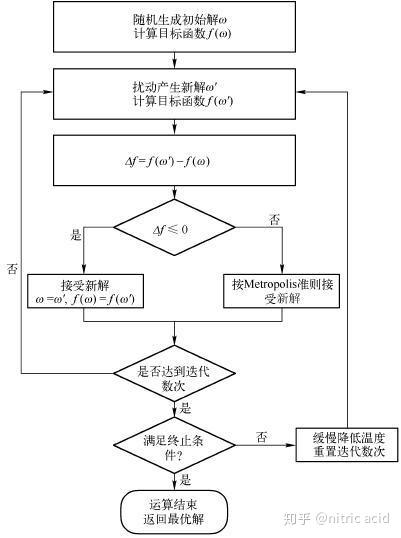
Step1 设定初始温度t=tmax, 任选初始解r=r0
Step2 内循环
Step2.1 从r的邻域中随机选一个解rt, 计算r和rt对应目标函 数值, 如rt对应目标函数值较小，则令r=rt; 否则若exp(-(E(rt)-E(r))/t)>random(0,1), 则令r=rt.
Step2.2 不满足内循环停止条件（1. 目标函数均值稳定 2. 连续若干步的目标值变化较小 3. 固定的抽样步数）时，重复Step2.1
Step3 外循环
Step3.1 降温t=decrease(t)
Step3.2 如不满足外循环停止条件，则转Step2（1. 达到终止温度 2. 达到迭代次数 3. 最优值连续若干步保持不变）；否则算法结束

其中，模拟退火算法新解的产生和接受的步骤：

第一步是由一个产生函数从当前解产生一个位于解空间的新解；为便于后续的计算和接受，减少算法耗时，通常选择由当前新解经过简单地变换即可产生新解的方法，如对构成新解的全部或部分元素进行置换、互换等，注意到产生新解的变换方法决定了当前新解的邻域结构，因而对冷却进度表的选取有一定的影响（冷却进度表(Cooling Schedule)包括控制参数的初值 t 及其衰减因子Δt 、每个 t 值时的迭代次数L和停止条件S）。

第二步是计算与新解所对应的目标函数差。因为目标函数差仅由变换部分产生，所以目标函数差的计算最好按增量计算。事实表明，对大多数应用而言，这是计算目标函数差的最快方法。

第三步是判断新解是否被接受,判断的依据是一个接受准则，最常用的接受准则是Metropolis准则: 若ΔT<0则接受S′作为新的当前解S，否则以概率exp(-ΔT/T)接受S′作为新的当前解S。

第四步是当新解被确定接受时，用新解代替当前解，这只需将当前解中对应于产生新解时的变换部分予以实现，同时修正目标函数值即可。此时，当前解实现了一次迭代。可在此基础上开始下一轮试验。而当新解被判定为舍弃时，则在原当前解的基础上继续下一轮试验。

模拟退火算法与初始值无关，算法求得的解与初始解状态S(是算法迭代的起点)无关；模拟退火算法具有渐近收敛性，已在理论上被证明是一种以概率l 收敛于全局最优解的全局优化算法；模拟退火算法具有并行性。

在已知的某个定义域内求函数最优值的问题通常有以下三种情况，以求最小值问题为例（求最大值可以转换为求最小值）：

· 如果是离散取值，则可以用穷举法获得问题最优解

· 如果取值连续，且函数是凸函数，则可以用梯度下降等方法获得最优解

· 如果连续非凸，虽说根据已有的近似求解法能够找到问题解，可解是否是最优的还有待考量，很多时候若初始值选择的不好，非常容易陷入局部最优值

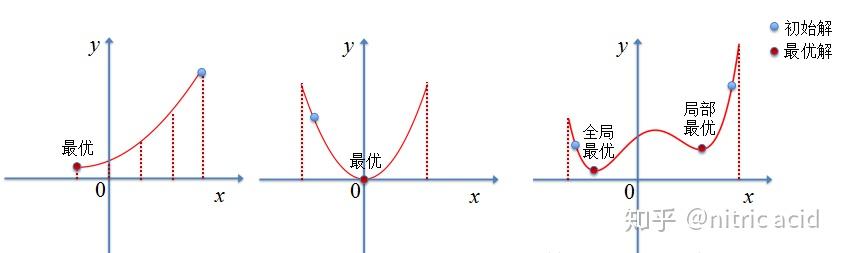
模拟退火算法就是为了应对第三种情况而提出的。

模拟退火算法的应用很广泛，可以高效地求解NP完全问题，如货郎担问题(Travelling Salesman Problem，简记为TSP)、最大截问题(Max Cut Problem)、0-1背包问题(Zero One Knapsack Problem)、图着色问题(Graph Colouring Problem)等等，但其参数难以控制，不能保证一次就收敛到最优值，一般需要多次尝试才能获得（大部分情况下还是会陷入局部最优值）。观察模拟退火算法的过程，发现其主要存在如下三个参数问题：

(1) 温度T的初始值设置问题

温度T的初始值设置是影响模拟退火算法全局搜索性能的重要因素之一、初始温度高，则搜索到全局最优解的可能性大，但因此要花费大量的计算时间；反之，则可节约计算时间，但全局搜索性能可能受到影响。

(2) 退火速度问题，即每个T值的迭代次数

模拟退火算法的全局搜索性能也与退火速度密切相关。一般来说，同一温度下的“充分”搜索是相当必要的，但这也需要计算时间。循环次数增加必定带来计算开销的增大。

(3) 温度管理问题

温度管理问题也是模拟退火算法难以处理的问题之一。实际应用中，由于必须考虑计算复杂度的切实可行性等问题，常采用如下所示的降温方式：

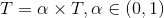
注：为了保证较大的搜索空间，α一般取接近于1的值，如0.95、0.9。