7 种不同优化器的选择技巧

前言

在机器学习中，当我们需要计算预测值和实际值之间的差距时，我们会使用所谓的损失函数（误差函数）。

虽然损失函数计算单个预测与其实际值的差距，但成本函数通常更通用。成本函数通常是训练集上所有的损失函数的平均值加上一些正则化的总和。

另一个经常被错误地用作前两个同义词的术语是目标函数，这是在训练期间优化的任何函数的最通用术语。

一旦弄清了正确的术语，我们就可以给出优化器的定义。

机器学习中的优化器用于调整神经网络的参数，以最小化损失函数。

因此，优化器的选择是一个重要的方面，可以评估我们训练的好坏。实际上，有很多可供选择的优化器，因此做出选择并不简单。在本文中，我将简要介绍最常用的优化器，然后为您提供一些在不同项目中对我有所帮助的指南，希望在为您的任务选择最合适的优化器时对您有所帮助。

有多少优化器？

正如刚才所说，有很多可供选择的优化器。他们每个都有各自优点和缺点，通常与特定任务相关。

我喜欢将优化器分为两个系列：梯度下降优化器和自适应优化器。这种划分完全基于操作方面，在梯度下降算法中强制您手动调整学习率，而在自适应算法中它会自动调整——这也是这个名字的来源。

梯度下降优化器

Batch gradient descent

Stochastic gradient descent

Mini-batch gradient descent

自适应优化器

Adagrad

Adadelta

RMSprop

Adam

梯度下降优化器

梯度下降优化器分为三种类型，它们的不同之处在于我们使用多少数据来计算目标函数的梯度。

Batch gradient descent

也称为 Vanilla 梯度下降，它是三者中最基本的算法。它计算目标函数 J 相对于整个训练集的参数 θ 的梯度。

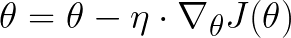
在批量梯度下降中更新权重。梯度乘以学习率 η，然后用于更新网络的参数

由于我们使用整个数据集只执行一个步骤，因此批量梯度下降可能会非常慢。此外，它不适用于数据集比内存大的情况。

Stochastic gradient descent

它是批量梯度下降的改进版本。它不是计算整个数据集的梯度，而是对数据集中的单个样本执行参数更新。因此，公式取决于输入 x 和输出 y 的值。

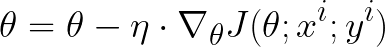
更新 SGD 权重

SGD 的问题在于更新比较频繁且方差大，因此目标函数在训练过程中波动较大。

这种波动对于批量梯度下降来说可能是一个优势，因为它允许函数跳到更好的局部最小值，但同时它每次迭代不同的样本，导致迭代方向变化很大，因此不能很快的收敛到局部最优解。

这个问题的一个解决方案是慢慢降低学习率值，以使更新越来越小，从而避免高振荡。

Mini-batch gradient descent

该算法利用我们目前所见的两种梯度下降方法的优点。它基本上计算小批量数据的梯度，以减少更新的方差。

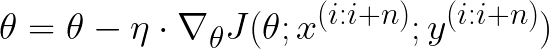
在小批量梯度下降中更新权重

要点 #1

• 在大多数情况下，小批量梯度下降是三者中的最佳选择。

• 学习率调整问题：所有这些都受制于选择一个好的学习率。不幸的是，对学习率的值的设定并不简单。

• 不适合稀疏数据：对罕见特征并不会区别对待，所有参数均等更新。

• 陷入局部最优的可能性很高。

自适应优化器

这个优化器家族被引入来解决梯度下降算法的问题。它们最重要的特点是不需要调整学习率值。实际上，一些库（例如Keras）——仍然允许您手动调整它以进行更高级的试验。

Adagrad

它让学习率适应参数，对常见的特征执行小更新，对罕见的特征执行大更新。

通过这种方式，网络更能够捕获属于不常见特征的信息，将它“特殊对待”并赋予正确的权重。

Adagrad 的问题在于它根据所有过去的梯度调整每个参数的学习率。因此，在训练很多步之后，学习率很有可能变得非常小 - 由于所有过去梯度的累积（两者非常相关）。

如果学习率太小，我们根本无法更新权重，网络的学习过程就陷入僵局。

Adadelta

和Adagrad不同，在训练过程中，该算法不再对历史梯度值进行单纯的累加，而是将其限制到固定尺寸w，从而有效地避免了学习率消失的问题。

RMSprop

它与 Adadelta 非常相似。唯一的区别在于它们对历史梯度数据的处理方式。

Adam

它结合了 Adadelta 和 RMSprop 的优势，存储过去梯度的指数衰减平均值（类似于动量）。

要点 #2

• 在大多数情况下，Adam 是自适应优化器中表现最好的。

• 适用于稀疏数据：自适应学习率非常适合此类数据集。

• 无需关注学习率值

梯度下降优化器与自适应优化器

一般来说，Adam 是最好的选择。无论如何，最近的许多论文都指出，如果结合良好的学习率衰减计划（训练期间），SGD 可以带来更好的结果。

我的建议是在任何情况下都先尝试 Adam，因为如果不进行高级微调，它更有可能返回良好的结果。

·? END? ·

HAPPY?LIFE