Authored by 谈谈天
『 最优化问题(也称为优化问题)泛指定量决策问题,主要关心如何对有限资源进行有效分配和控制,并达到某种意义上的最优。 』
最优化的关键技能包括:
『 Good structure leads to good properties,and good properties can result in wide applications. 』
最优化问题一般可描述为
其中, 是决策变量;
是目标函数;
是约束集合或可行域;记号s.t. 是“subject to”的缩写,专指约束条件。
最优化模型与算法相辅相成,促进最优化学科不断发展。实际应用导出的各种各样的最优化模型给最优化学科不断注入新鲜的血液,对现有的优化算法进行挑战并推动其向前发展;最优化算法的设计及理论分析帮助实际问题建立更鲁棒稳定的模型。
通常地,最优化问题有以下分类方式:
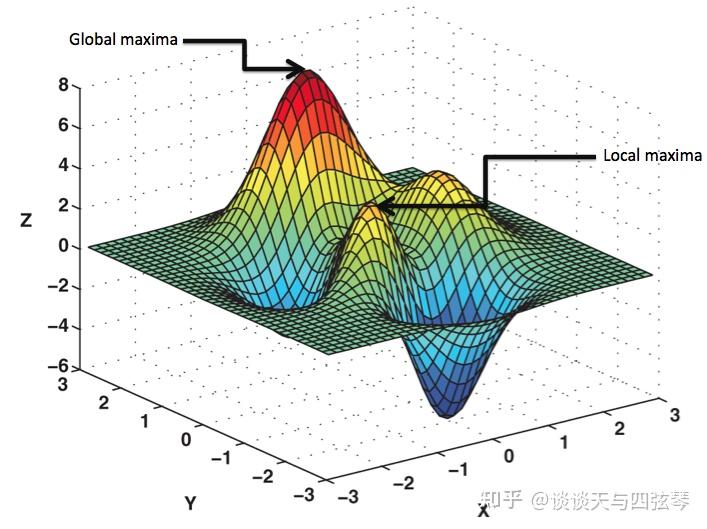
针对模型 ,对于可行点
(即
),
- 如果 ,那么称
为问题
的全局极小解(点),有时也称为(全局)最优解或最小值点;
- 如果存在 的一个
邻域
,使得
,那么称
为问题
的局部极小解(点),有时也称为局部最优解;
- 进一步地,如果 成立,则称
为问题
的严格局部极小解(点)。
现实中,最优化具备广泛的应用,可谓“万物皆优化”:
深度学习,强化学习,压缩感知,最优运输,金融工程,电力系统,物流服务,
面对一个优化问题,我们有诸多方法进行求解。下面的两张图,展示了我个人梳理的一个分类。

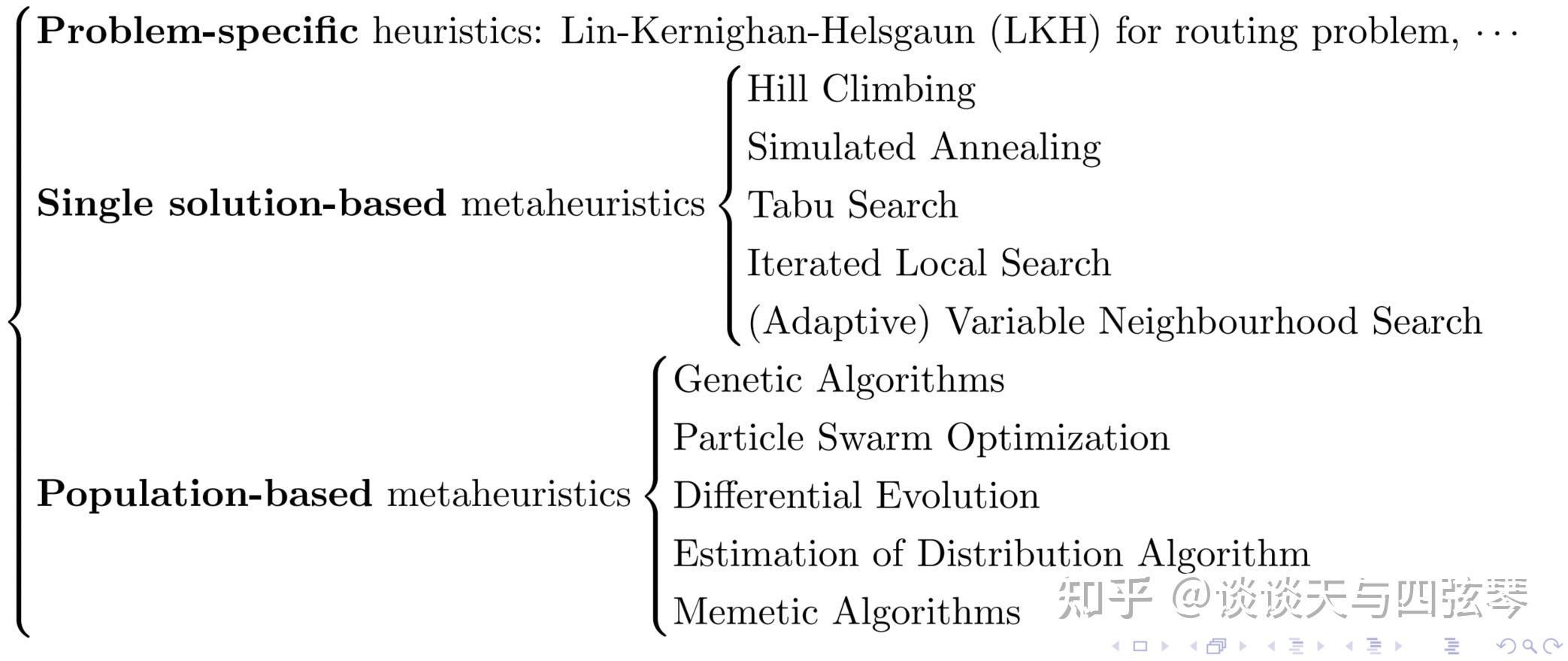
图2、3展示了我对优化问题求解方法的分类,包括:精确算法、(元)启发式算法、新兴学习算法。
『 精确算法 』是最为经典的优化方法,大致可以分为连续和离散/组合两大类。这里着重讨论处理离散/组合类问题的方法,事实上,离散/组合类问题相比于连续问题更加困难。对于此类问题,本质上只能通过隐枚举法或枚举法的思想来求解问题,例如分支定界法(Branch-and-Bound, BB)就是一种隐枚举法。在此基础上,可以动态地增加相应线性规划模型的有效不等式(切),这即是分支定切法(Branch-and-Cut)。若是不加切,而是将相应的线性规划模型转化为等价的Dantzig-Wolfe模型,进而利用列生成(Column generation)方法进行求解,则是分支定价法(Branch-and-Price)。
另外,由于商业/开源求解器(Solver)的日益成熟与强大,我将其单独划分为“一类”。求解器是优化方法与软件工程交融的技术结晶,其中商用的翘楚包括Gurobi、CPLEX以及国产的COPT等,开源的则有SCIP等。除此之外,还有一些领域专用求解器,例如为求解TSP问题服务的Concorde。Concorde目前在公开TSP数据集中,获得了其中110个数据的最优解记录,其中最多的TSP位置点达到了85900个。这样的规模,很难不让一些启发式算法和学习算法汗颜。
『(元)启发式算法 』启发式算法是搜索算法的典型代表之一,在运算过程中利用有效的经验法则来改进给定的可行解,其能较快得到较好的可行解,但解的质量相较于最优解而言存在一定的未知性。更详细的分类见图3。首先是Problem-specific heuristics,这是一类针对特定问题设计的启发式算法,例如TSP、VRP这类路由问题中著名的Lin-Kernighan-Helsgaun (LKH) 算法,其具备精巧的设计,在论文中也是非常强大的baseline的存在。然而,现实中的优化问题灿若繁星,并非每一个都有LKH这么优秀的算法。为了在有限的时间与计算资源下有效求解这些问题,学者们通过模拟一些自然规律(如适者生存,金属冶炼,鸟群飞行等),设计了一系列智能算法,这些算法也称为元启发式算法(Metaheuristic)。
Metaheuristic是优化领域的主要研究分支之一,包罗众多成果。进一步地,我们可以将其分为两类,Single solution-based和Population-based。正如其名,Single solution-based的算法依据问题结构编码一个初始解,并设计一些“不断向好”的更新规则,更新当前的解。爬山法(Hill Climbing)是其中的代表性算法。然而,回顾图1中的Landscape,设想我们在最左侧放置一个小球(对应一个初始解),其会落入局部极小解的“山谷”而无法进一步找到全局极小解。再者,若将小球放入右侧的“高原(Plateau)”,其将不会进一步滚动(对应优化)。为了避免这种情况的发生,在优化初期,我们会依一定概率 容许对较差解的“探索(Exploration)”,而在优化后期不断加强“开发(Exploitation)”,如此赋予算法“跳出”局部极小解的能力。这也是著名的模拟退火(Simulated Annealing)算法的思想。
根据上述分析,我们或许可以想到,如果同时放置很多小球(对应多个初始解),应该可以提高找到全局极小解的概率。的确,这多个初始解够成了一个解的种群,这类算法也被划分为Population-based。其代表性算法包括更擅长处理连续优化问题的粒子群算法(Particle Swarm Optimization)、差分进化算法(Differential Evolution),和更擅长处理离散/组合优化问题的遗传算法(Genetic Algorithms)、分布估计算法(Estimation of Distribution Algorithm)等。这个领域的最新进展,可以关注一些领域顶级刊物和会议:IEEE Transactions on Evolutionary Computation, IEEE Computational Intelligence Magazine, Evolutionary Computation, IEEE Transactions on Cybernetics, IEEE Transactions on Emerging Topics in Computational Intelligence, Swarm and Evolutionary Computation, IEEE CEC, ACM GECCO等。
『 新兴学习算法 』
伴随着机器学习等新兴技术的巨大成功,涌现了这类新的优化技术。具体做法很多,这里列举三个。
第一类:Data-driven metaheuristic[4]。旨在引入机器学习技术,为(元)启发式算法领域带来新的活力。
Data-Driven Evolutionary Optimization第二类:ML4CO[5]。可参考我写过的一篇知乎回答:
运筹学与机器学习结合前景如何?第三类:Predict-then-Optimize (PTO),“预测+优化”。
运筹OR帷幄:优化|当机器学习上运筹学:PyEPO与端对端预测后优化值得说明的是,针对同一实际问题,从不同的设计角度切入,可以对应性质很不相同的问题,其求解难度和需要的算法也将差别很大。
例如,在投资组合优化(Portfolio Optimization)问题中,人们总体上希望通过寻求最优的投资组合以降低风险、提高收益。
在设计优化算法时,我们有一些基本的准则或技巧。对于复杂的优化问题,基本的想法是将其转化为一系列简单的优化问题(其最优解容易计算或者有显式表达式)来逐步求解。 典型技巧有:
可以拆分成
参考文献
[1]Stephen Boyd and Lieven Vandenberghe. Convex Optimization. Cambridge University Press, 2004.
[2]文再文等. 最优化:建模、算法与理论. 高等教育出版社, 2020.
[3]殷允强,王杜娟,余玉刚. 整数规划:基础、扩展及应用. 科学出版社, 2022.06 First Edition.
[4]Jin, Y., Wang, H., & Sun, C. Data-Driven Evolutionary Optimization. Springer, 2021.
[5]郭田德,韩丛英,唐思琦. 组合优化机器学习方法. 科学出版社, 2019.11 First Edition.