35 最优化问题

时间：2024-06-04 16:19:10 浏览：次

在统计计算中广泛用到求最小（最大）值点或求方程的根的算法，比如，参数最大似然估计、置信区间的统计量法、回归分析参数估计、惩罚似然估计、惩罚最小二乘估计，等等。求最小值点或最大值点的问题称为最优化问题（或称优化问题），最优化问题和求方程的根经常具有类似的算法，所以在这一章一起讨论。有些情况下，可以得到解的解析表达式；更多的情况只能通过数值迭代算法求解。

这一部分将叙述最小值点存在性的一些结论，并给出一些常用的数值算法。还有很多的优化问题需要更专门化的算法。关于最优化问题的详细理论以及更多的算法，读者可以参考这方面的教材和专著，如高立 (2014), 刘浩洋 et al. (2020)，Kochenderfer (2019), Lange (2013), 徐成贤, 陈志平, and 李乃成 (2002) 。

因为求最大值的问题和求最小值的问题完全类似，而且最小值问题涉及到凸函数、正定海色阵等，比最大值问题方便讨论，所以我们只考虑最小值问题。

设$f(\boldsymbol x)$是$\mathbb R^d$上的多元函数，如果$f(\boldsymbol x)$有一阶偏导数，则记$f(\boldsymbol x)$的梯度向量为 \[\begin{aligned} abla f(\boldsymbol x)=\left( \frac{\partial f(\boldsymbol x)}{\partial x_1}, \frac{\partial f(\boldsymbol x)}{\partial x_2}, \dots, \frac{\partial f(\boldsymbol x)}{\partial x_d} \right)^T, \end{aligned}\] 有的教材记梯度向量为$\boldsymbol g(\boldsymbol x)$。如果$f(\boldsymbol x)$的二阶偏导数都存在，则记它的海色阵为 \[\begin{aligned} abla^2 f(\boldsymbol x)=\left( \frac{\partial^2 f(\boldsymbol x)}{\partial x_i \partial x_j} \right)_{\substack{i=1,\dots,d\\j=1,\dots,d}} \ , \end{aligned}\] 有的教材记海色阵为$H_f(\boldsymbol x)$或$H(x)$。当所有二阶偏导数连续时，海色阵是对称阵。

定义35.1 (无约束最优化) 设$f(\boldsymbol x), \boldsymbol x=(x_1, \dots, x_d)^T \in \mathbb R^d$是实数值的$d$元函数，求 \[\begin{aligned} \mathop{ ext{argmin}}\limits_{\boldsymbol x \in \mathbb R^d } f(\boldsymbol x) \end{aligned}\] 的问题称为（全局的）无约束最优化问题。

这里，符号$ ext{argmin}$表示求最小值点的运算, 称$f(\boldsymbol x)$为目标函数，自变量$\boldsymbol x$称为决策变量。 $\boldsymbol x^*$是问题的解等价于 \[\begin{aligned} f(\boldsymbol x) \geq f(\boldsymbol x^*), \ \forall \boldsymbol x \in \mathbb R^d, \end{aligned}\] 称这样的$\boldsymbol x^*$为$f(\boldsymbol x)$的一个全局最小值点。全局最小值点不一定存在，存在时不一定唯一。如果 \[\begin{align*} f(\boldsymbol x) > f(\boldsymbol x^*), \ \forall \boldsymbol x \in \mathbb R^d \backslash \{\boldsymbol x^* \}, \end{align*}\] 则称$\boldsymbol x^*$为$f(\boldsymbol x)$的一个全局严格最小值点, 全局严格最小值点如果存在一定只有一个。上式中“$\backslash$”表示集合的差。

对$\boldsymbol x \in \mathbb R^d$和$\delta>0$，定义 \[ U(\boldsymbol x, \delta)=\{ \boldsymbol y \in \mathbb R^d:\; \| \boldsymbol y - \boldsymbol x \| < \delta \}, \] 称为$\boldsymbol x$的邻域或开邻域，定义 \[ U_0(\boldsymbol x, \delta)=\{ \boldsymbol y \in \mathbb R^d:\; \| \boldsymbol y - \boldsymbol x \| < \delta, \boldsymbol y eq \boldsymbol x \}, \] 为$\boldsymbol x$的空心开邻域。

如果存在$\boldsymbol x^*$的开邻域$U(\boldsymbol x, \delta)$使得 \[ f(\boldsymbol x) \geq f(\boldsymbol x^*), \ \forall \boldsymbol x \in U(\boldsymbol x, \delta), \] 称$\boldsymbol x^*$是$f(\boldsymbol x)$的一个局部极小值点；如果存在$\boldsymbol x^*$的空心开邻域$U_0(\boldsymbol x, \delta)$使得 \[ f(\boldsymbol x) > f(\boldsymbol x^*), \ \forall \boldsymbol x \in U_0(\boldsymbol x, \delta), \] 称$\boldsymbol x^*$是$f(\boldsymbol x)$的一个局部严格极小值点。

定义35.2 (约束最优化) 设$c_i(\cdot)$, $i=1,\dots,p+q$是$d$元实值函数, 求 \[\begin{align} \begin{cases} & \mathop{ ext{argmin}}\limits_{\boldsymbol x \in \mathbb R^d } f(\boldsymbol x), \ ext{s.t.} \\ & c_i(\boldsymbol x)=0, \ i=1,\dots,p \\ & c_i(\boldsymbol x) \leq 0, \ i=p+1, \dots, p+q \end{cases} ag{35.1} \end{align}\] 的问题称为（全局的）约束最优化问题, 这里s.t.(subject to)是“满足如下约束条件”的意思, $c_i, i=1,\dots,p$称为等式约束， $c_i, i=p+1, \dots, p+q$称为不等式约束。满足约束的$\boldsymbol x \in \mathbb R^d$称为一个可行点, 所有可行点的集合$D$称为可行域: \[\begin{align*} D=\{ \boldsymbol x \in \mathbb R^d:\ c_i(\boldsymbol x)=0, i=1,\dots,p; \ c_i(\boldsymbol x) \leq 0, i=p+1, \dots, p+q \}. \end{align*}\]

最优化问题(35.1)也可以写成$\min\limits_{\boldsymbol x \in D} f(\boldsymbol x)$。若$\boldsymbol x^* \in D$使得 \[\begin{align*} f(\boldsymbol x) \geq f(\boldsymbol x^*), \ \forall \boldsymbol x \in D, \end{align*}\] 称$\boldsymbol x^*$为约束优化问题(35.1)的一个全局最小值点。如果$\boldsymbol x^* \in D$使得 \[\begin{align*} f(\boldsymbol x) > f(\boldsymbol x^*), \ \forall \boldsymbol x \in D \backslash \{ \boldsymbol x^* \}, \end{align*}\] 称$\boldsymbol x^*$为约束优化问题(35.1)的一个全局严格最小值点。

如果$\boldsymbol x^* \in D$且存在$\boldsymbol x^*$的开邻域$U(\boldsymbol x, \delta)$使得 \[ f(\boldsymbol x) \geq f(\boldsymbol x^*), \ \forall \boldsymbol x \in U(\boldsymbol x, \delta) \cap D, \] 称$\boldsymbol x^*$是约束优化问题(35.1)的一个局部极小值点；如果$\boldsymbol x^* \in D$且存在$\boldsymbol x^*$的空心开邻域$U_0(\boldsymbol x, \delta)$使得 \[ f(\boldsymbol x) > f(\boldsymbol x^*), \ \forall \boldsymbol x \in U_0(\boldsymbol x, \delta) \cap D, \] 称$\boldsymbol x^*$是约束优化问题(35.1)的一个局部严格极小值点。

最优化问题经常使用数值迭代方法求解，数值迭代方法大多要求每一步得到比上一步更小的目标函数值，这样最后迭代结束时往往得到的不是全局的最小值点，而是局部的极小值点。要注意的是，全局的最小值点一定也是局部极小值点, 另外，极小值点有时不存在，存在时可以不唯一。本书中的最优化算法一般只能收敛到局部极小值点。

因为等式约束$c_i(\boldsymbol x)=0$可以写成两个不等式约束： \[ c_i(\boldsymbol x) \leq 0, \quad -c_i(\boldsymbol x) \leq 0, \] 所以约束优化问题(35.1)有时写成如下的简化形式： \[\begin{align} \begin{cases} & \mathop{ ext{argmin}} \limits_{\boldsymbol x \in \mathbb R^d } f(\boldsymbol x), \ ext{s.t.} \\ & c_i(\boldsymbol x) \leq 0, \ i=1,\dots,p \end{cases}, ag{35.2} \end{align}\] 可行域为 \[\begin{align*} D=\{ \boldsymbol x \in \mathbb R^d:\; c_i(\boldsymbol x) \leq 0, i=1,\dots,p \} . \end{align*}\]

例35.1 函数$f(x)=\frac{1}{1 + x^2}, x \in \mathbb R$没有极小值点， $f(x) > 0$, $\lim_{x o\pm\infty} f(x)=0$。

例35.2 函数$f(x)=\max(|x|, 1)$最小值为1, 且当$x \in [-1, 1]$时都取到最小值。

在最优化问题中如果要求解$\boldsymbol x$的所有或一部分分量取整数值，这样的问题称为整数规划问题。如果要同时考虑具有相同自变量的多个目标函数的优化问题，则将其称为多目标规划问题。对约束最优化问题(35.1)，如果$f(\boldsymbol x), c_i(\boldsymbol x)$都是线性函数，称这样的问题为线性规划问题。线性规划是运筹学的一个重要工具，在工业生产、经济计划等领域有广泛的应用。如果(35.1)中的$f(\boldsymbol x), c_i(\boldsymbol x)$不都是线性函数，称这样的问题为非线性规划问题。对非线性规划问题，如果$f(\boldsymbol x)$是二次多项式函数， $c_i(\boldsymbol x)$都是线性函数，称这样的问题为二次规划问题。本书主要讨论在统计学中常见的优化问题，不讨论线性规划、整数规划、多目标规划等问题。

最优化是统计计算中最常用的工具之一，另外常用的是随机模拟和积分，矩阵计算也是统计计算中最基本的组成部分。

许多统计方法的计算都归结为一个最优化问题。比如，在估计问题中，最大似然估计和最小二乘估计都是最优化问题。在试验或者抽样调查方案的设计时，也需要用最优化方法制作误差最小的方案。在现代的深度神经网络等机器学习方法中，也要用最优化方法训练模型。

最常见的统计模型是回归问题 \[\begin{align} y=f(\boldsymbol x; \boldsymbol heta) + \varepsilon , ag{35.3} \end{align}\] 其中$\boldsymbol heta$是未知的不可观测但非随机的模型参数， $\varepsilon$是随机误差，模型拟合归结到估计$\boldsymbol heta$的问题。

函数$f$最简单的是线性函数，模型(35.3)变成 \[\begin{align} y=\boldsymbol x^T \boldsymbol\beta + \varepsilon , ag{35.4} \end{align}\] 其中$\boldsymbol\beta$是未知参数， $\varepsilon$服从正态分布。模型的样本为$(\boldsymbol x_i, y_i), i=1,2,\dots,n$, 在估计模型参数$\boldsymbol\beta$时，认为$\boldsymbol\beta$是客观存在的未知、非随机值，先用一个变量$\boldsymbol b$代替$\boldsymbol\beta$，定义拟合误差 \[ r_i(\boldsymbol b)=y_i - \boldsymbol x_i^T \boldsymbol b , \] 按照某种使得拟合误差最小的准则求一个$\boldsymbol b$ 作为真实参数$\boldsymbol\beta$的估计值。注意拟合误差$r_i(\boldsymbol b)$是样本与变量$\boldsymbol b$的函数，这既不是随机误差$\varepsilon_i=y_i - \boldsymbol x_i^T \boldsymbol\beta$，也不是$\varepsilon_i$的观测值（$\varepsilon_i$是不可观测的）。

因为拟合误差有$n$个，需要定义某种规则才能同时最小化$n$个拟合误差。一个自然的考虑是最小化各个拟合误差绝对值的总和： \[ R_1(\boldsymbol b)=\sum_{i=1}^n | y_i - \boldsymbol x_i^T \boldsymbol b | , \] 但是这个函数关于$\boldsymbol b$不可微，最优化的数值算法也比较复杂，所以通常考虑最小化拟合误差的平方和： \[ R_2(\boldsymbol b)=\sum_{i=1}^n | y_i - \boldsymbol x_i^T \boldsymbol b |^2=\sum_{i=1}^n \left( y_i - \boldsymbol x_i^T \boldsymbol b \right)^2 , \] 此函数是$\boldsymbol b$的二次多项式函数，必存在最小值点且适当条件下最小值点有显式解。最小二乘估计就是如下的无约束最优化问题 \[\begin{align} \min_{\boldsymbol b} \sum_{i=1}^n \left( y_i - \boldsymbol x_i^T \boldsymbol b \right)^2 . ag{35.5} \end{align}\]

最小二乘问题也可能会是带有约束的，比如在线性回归中要求$\boldsymbol\beta$中的各个回归系数非负，记作$\boldsymbol\beta \succeq \boldsymbol 0$，估计$\boldsymbol\beta$就变成了约束最小二乘问题 \[ \min_{\boldsymbol b \succeq \boldsymbol 0} \sum_{i=1}^n \left( y_i - \boldsymbol x^T \boldsymbol b \right)^2 . \] 约束优化问题比无约束优化问题困难得多，也不存在显式解。

回归模型也可以是非线性的，这时最小二乘问题为 \[ \min_{\boldsymbol t} \sum_{i=1}^n \left( y_i - f(\boldsymbol x_i; \boldsymbol t) \right)^2 , \] 此问题比线性模型的最小二乘问题困难，一般也没有解的表达式。

在$R_1(\cdot)$中用$|r_i(\boldsymbol b)|$度量误差大小，在$R_2(\cdot)$中用$r_i^2(\boldsymbol b)$度量误差大小，也可以将误差大小的度量推广为一般的$\rho(r_i(\boldsymbol b))$，其中$\rho(z)$随$|z|$增大而增大。模型估计转换为如下的最优化问题 \[\begin{align} \min_{\boldsymbol t} \sum_{i=1}^n \rho(y_i - f(\boldsymbol x_i; \boldsymbol t)) , ag{35.6} \end{align}\] 这一般比最小二乘在理论上和计算上都复杂得多。

不同的观测可能具有不同的误差大小，在最小化拟合误差时可以给不同的观测加不同的权重，误差大的观测权重小，估计问题变成如下最优化问题： \[\begin{align} \min_{\boldsymbol t} \sum_{i=1}^n w(y_i, \boldsymbol x_i, \boldsymbol t) \rho(y_i - f(\boldsymbol x_i; \boldsymbol t)) , ag{35.7} \end{align}\] 其中$w(y_i, \boldsymbol x_i, \boldsymbol t)$是第$i$个观测的权重，经常不直接依赖于观测值和参数变量，所以往往写成$w_i$。例如，线性模型的加权最小二乘估计： \[ \min_{\boldsymbol b} \sum_{i=1}^n w_i \left( y_i - \boldsymbol x_i^T \boldsymbol b \right)^2 , \] 这个问题也有显式解。

在现代的对回归问题的研究中，又提出了对估计施加某种惩罚的做法，目的是克服过拟合问题。估计问题变成如下最优化问题： \[\begin{align} \min_{\boldsymbol t} \sum_{i=1}^n w(y_i, \boldsymbol x_i, \boldsymbol t) \rho(y_i - f(\boldsymbol x_i; \boldsymbol t)) + \lambda g(\boldsymbol t) , ag{35.8} \end{align}\] 其中$g(\cdot)$是对估计参数的复杂程度的一种取非负值的惩罚函数， $\lambda > 0$是调整估计的模型的复杂程度的一个调节因子。例如，岭回归问题对应于如下的最优化问题： \[ \min_{\boldsymbol b} \left\{ \sum_{i=1}^n \left( y_i - \boldsymbol x_i^T \boldsymbol b \right)^2 + \lambda \boldsymbol b^T \boldsymbol b \right\} , \] 此惩罚倾向于产生分量的绝对值较小的估计$\boldsymbol b$。 Lasso回归实际是如下的最优化问题： \[ \min_{\boldsymbol b} \left\{ \sum_{i=1}^n \left( y_i - \boldsymbol x_i^T \boldsymbol b \right)^2 + \lambda \| \boldsymbol b \|_1 \right\} , \] 其中$\| \boldsymbol b \|_1=\sum_{j=1}^p | b_j |$。此惩罚倾向于产生分量的绝对值较小的估计$\boldsymbol b$，而且$\lambda$较大时会使得参数估计$\boldsymbol b$的部分分量退化到0。

模型(35.3)中的$f$是形式已知，参数$\boldsymbol heta$未知的。还可以认为$f(\cdot)$是未知的，直接用一个函数$ ilde f(\cdot)$来近似$f$。这称为非参数回归。但是，如果仅要求$y_i - ilde f(\boldsymbol x)$小，有许多函数可以使得这些拟合误差完全等于零（当相同的$\boldsymbol x$都对应相同的$y$）时。所以，必须对$ ilde f$施加一定的限制，称为正则化(regularization)。比如，要求$ ilde f$二阶连续可微且比较“光滑”，最优化问题变成 \[ \min_{ ilde f ext{ 二阶连续可微}} \sum_{i=1}^n (y_i - ilde f(\boldsymbol x_i))^2 + \lambda \int [ ilde f''(\boldsymbol x)]^2 \, d\boldsymbol x . \] $\lambda>0$是光滑度的调节参数， $\lambda$越大，最后得到的回归函数估计$ ilde f$越光滑。

参数估计问题中，最大似然估计是将观测的联合密度函数或者联合概率函数看成是未知参数的函数，称为似然函数, 通过最大化似然函数来估计参数。

在(35.3)的估计中，除了可以最小化残差的方法，还可以用最大似然估计方法。设$\varepsilon$有密度函数$p(\cdot)$, 且各个观测相互独立，则参数$\boldsymbol heta$的最大似然估计问题是 \[ \max_{\boldsymbol t} \prod_{i=1}^n p(y_i - f(\boldsymbol x_i; \boldsymbol t)) . \] 但这样的优化问题可能很难计算求解。对某些密度$p(\cdot)$, 最大似然估计与最小化拟合残差是等价的。

如果$f(\cdot)$是非参数的未知回归函数，也可以用最大似然估计求解，但仍需要施加正则化，如 \[ \max_{f ext{ 二阶连续可微}} \ \prod_{i=1}^n p(y_i - f(\boldsymbol x_i; \boldsymbol t)) \;\exp\left\{-\lambda \int [f''(\boldsymbol x)]^2 \, d\boldsymbol x \right\} . \]

许多统计问题的解归结为一个最优化问题。但是，产生的最优化问题会有解的存在性、唯一性、局部最优等问题。要解决的统计问题与要解决的最优化问题应该是一致的，不能因为可以求解的最优化问题的限制而修改原来的统计问题。由于约束优化问题的特点，最优值常常在边界处达到，所以用优化问题求解统计模型对模型的假定更为敏感，数据不满足某些模型假定时用最优化方法解出的结果可能不能很好地解释数据。

许多统计问题需要同时对多个目标优化，或在某些约束下优化，这就需要适当地设计策略，不同策略产生不同的统计方法。最简单的做法是对各个目标或约束的加权和进行优化。

先复习一些数学分析中的结论。设$f(x)$为定义在闭区间$[a, b]$上的连续函数，则$f(x)$在$[a, b]$内有界，且能达到最小值和最大值, 极值可以在区间内部或边界取到。设$f(x)$在区间$(a,b)$（有限或无限区间）可微。

定理35.1 (一阶必要条件) 若$x^* \in (a,b)$是$f(x)$的一个局部极小值点，则$f'(x^*)=0$。

这只是必要条件，不是充分条件。局部极大值点也满足同样的条件。满足$f'(x^*)=0$的$x^*$叫做$f(x)$的一个稳定点，它可能是局部极小值点、局部极大值点，也可能不是局部极值点。证明略。

定理35.2 (二阶必要条件) 若$f(x)$在$(a,b)$内有二阶导数， $x^* \in (a,b)$是$f(x)$的一个局部极小值点，则$f'(x^*)=0$且$f''(x^*) \geq 0$。

这可以用下面的二阶充分条件来证明。对局部极大值点，条件$f''(x^*) \geq 0$变成了$f''(x^*) \leq 0$。

定理35.3 (二阶充分条件) 若$f(x)$在$(a,b)$内有二阶导数，对$x^* \in (a,b)$同时有$f'(x^*)=0$且$f''(x^*) > 0$，则$x^*$是$f(x)$的一个局部极小值点。

若$f'(x^*)=0$且$f''(x^*) < 0$则$x^*$是局部极大值点。当$f''(x^*)=0$时，不能确定$x^*$是否极值点。

当一元连续函数$f(x)$的定义域为区间但不是闭区间时， $f(x)$在定义域内不一定取到最小值，通常可以通过检查边界处的极限并与内部的所有极小值的比较来确定。

例35.3 对$f_1(x)=x^2, x \in \mathbb R$, $x^*=0$使得$f_1'(x^*)=2x^*=0$, $f_1''(x^*)=2>0$，是一个局部极小值点。因为$x^*=0$是唯一的极小值点，当$x o \pm\infty$时函数值增大，所以这个局部极小值点也是全局最小值点。

对$f_2(x)=x^3$, $x^*=0$使得$f_2'(x^*)=3 (x^*)^2=0$, 是一个稳定点。但是$f_2''(x^*)=6 x^*=0$，不能保证$x^*$是极值点。事实上，$x^*=0$不是$f_2(x)=x^3$的极值点。

对$f_3(x)=\frac{1-x}{1 + x^2}, x \geq 0$, 有$f_3(0)=1$, $\lim_{x o+\infty} f_3(x)=0$, $f_3'(x)=\frac{x^2 - 2x - 1}{(x^2 + 1)^2}$, 令$f_3'(x)=0$得稳定点$x^*=1 + \sqrt{2}$，且$f_3(x^*)=-\sqrt{2}/(4 + 2\sqrt{2})<0$，所以$x^*$是$f_3(x)$的全局最小值点。

例35.4 存在不可微点时极值点也不一定出现在稳定点。例如，设总体$X \sim ext{U}(0, b)$, 样本$X_1, \dots, X_n$, 似然函数为 \[\begin{aligned} L(b)=& \prod_{i=1}^n \frac{1}{b} I_{[0,b]}(X_i)=\frac{1}{b^n} I_{[0,b]}(X_{(n)}), \end{aligned}\] 其中$X_{(n)}=\max(X_1, \dots, X_n)$。导数 \[\begin{aligned} L'(b)=& \begin{cases} 0 & b < X_{(n)}, \\ ext{不存在}, & b=X_{(n)}, \\ -n b^{-n-1}, & b > X_{(n)}, \end{cases} \end{aligned}\] $L(b)$的最大值点为$\hat b=X_{(n)}$，$L'(\hat b)$不存在。

定义35.3 (凸集) 设$S$是$\mathbb R^d$的子集，如果$\forall \boldsymbol x, \boldsymbol y \in S$, $\alpha \in [0, 1]$, 都有$\alpha \boldsymbol x + (1-\alpha) \boldsymbol y \in S$，则称$S$为凸集。

等价地，若对任意正整数$n \geq 2$ 和$S$中的$n$个互不相同的点$\boldsymbol x^{(j)}, j=1,2,\dots,n$，以及任意的$\{ \alpha_j, j=1,\dots,n \}$满足 $\alpha_j \geq 0, \sum_{j=1}^n \alpha_j=1$都有 $\sum_{j=1}^n \alpha_j \boldsymbol x^{(j)} \in S$，则$S$是凸集。

$S$是凸集当且仅当$S$中任意两个点的连线都属于$S$。例如，实数轴上的凸集和区间是等价的; 平面上边界为椭圆、三角形、平行四边形的集合是凸集, 圆环则不是凸集; 球体、长方体是凸集。

定义35.4 (凸壳) 设$A$是$\mathbb R^d$的子集，称包含$A$的最小的凸集$S$为$A$的凸壳。

$A$的凸壳的等价定义为 \[\begin{aligned} ext{conv}(A)=& \left\{ \sum_{i=1}^m \alpha_i \boldsymbol x_i: m=1,2,\dots; \right. \\ & \quad\left. \boldsymbol x_i \in A, \alpha_i \geq 0, i=1,2,\dots, m, \sum_{i=1}^m \alpha_i=1 \right\} \end{aligned}\]

凸集有如下性质:

凸集的闭包是凸集。
凸集的内核（所有内点组成的集合）是凸集。
凸集是连通集合。
任意多个凸集的交集是凸集。
关于仿射变换$f(\boldsymbol x)=A \boldsymbol x + \boldsymbol b$($A$为矩阵, $\boldsymbol b$为常数向量)，凸集的像和原像还是凸集。
两个凸集$S, T$的笛卡尔积$S imes T=\{ (\boldsymbol x, \boldsymbol y): \boldsymbol x \in S, \boldsymbol y \in T \}$是凸集。
设$S$是$\mathbb R^d$中的凸集，$\lambda$为实数，则$\lambda S \stackrel{ riangle}{=} \{\boldsymbol y \in \mathbb R^d: \boldsymbol y=\lambda \boldsymbol x, \boldsymbol x \in S \}$是凸集。
设$S, T$是$\mathbb R^d$中的两个凸集，则 $S + T \stackrel{ riangle}{=} \{\boldsymbol z \in \mathbb R^d: \boldsymbol z=\boldsymbol x + \boldsymbol y, \boldsymbol x \in S, \boldsymbol y \in T \}$是凸集。
对$\mathbb R^d$的凸集$S$以及任意$\boldsymbol y \in \mathbb R^d$, 令$\boldsymbol y$到$S$的距离为 $ ext{dist}(\boldsymbol y, S) \stackrel{ riangle}{=} \inf_{\boldsymbol x \in S} \| \boldsymbol y - \boldsymbol x \|$, 则至多有一个$\boldsymbol x_0 \in S$可以满足$\| \boldsymbol y - \boldsymbol x_0 \|= ext{dist}(\boldsymbol y, S)$。当$S$是闭的凸集时，存在唯一的$\boldsymbol x_0 \in S$使得$\| \boldsymbol y - \boldsymbol x_0 \|= ext{dist}(\boldsymbol y, S)$。
设$S$为凸集，$\boldsymbol x_0$是$S$的边界点，则存在单位向量$\boldsymbol v \in \mathbb R^d$使得$\boldsymbol v^T \boldsymbol x_0 \geq \boldsymbol v^T \boldsymbol x, \forall \boldsymbol x \in S$。

定义35.5 (凸函数) 定义在凸集$S$上的$d$元函数$f(\boldsymbol x)$称为凸函数, 如果对任意$\boldsymbol x, \boldsymbol y \in S$和$\alpha \in [0, 1]$都有 \[\begin{align} f( \alpha \boldsymbol x + (1 - \alpha) \boldsymbol y) \leq \alpha f(\boldsymbol x) + (1 - \alpha) f(\boldsymbol y), ag{35.9} \end{align}\] 如果(35.9)对任意$\boldsymbol x eq \boldsymbol y \in S$和$\alpha \in (0,1)$ 都满足严格不等式，则称$f(\boldsymbol x)$为严格凸函数。

若$-f(\boldsymbol x)$是定义在凸集$S$上的凸函数，则称$f(\boldsymbol x)$为凹函数。

对凸函数$f(\boldsymbol x)$，设$\boldsymbol x^{(j)}, j=1,\dots, n$是$S$中的$n$个点， $\alpha_j \geq 0, j=1,\dots,n$, $\sum_{j=1}^n \alpha_j=1$，则 \[\begin{aligned} f\left(\sum_{j=1}^n \alpha_j \boldsymbol x^{(j)} \right) \leq \sum_{j=1}^n \alpha_j f(\boldsymbol x^{(j)}). \end{aligned}\]

设$f(\boldsymbol x)$是正值函数，如果$\log f(\boldsymbol x)$是凸函数，则称$f(\boldsymbol x)$为对数凸函数。

例35.5 所有的范数（模）都是凸函数。

下面给出凸函数的另外一些性质。

设$S$是$\mathbb R^d$的凸集， $f(\boldsymbol x), \boldsymbol x \in S$是凸函数当且仅当 $\{(\boldsymbol x, y):\ f(\boldsymbol x) \leq y, \;\boldsymbol x \in S, y \in \mathbb R \}$是凸集。
若$f(\boldsymbol x)$是定义在$\mathbb R^d$的开凸集$S$上的可微函数，则$f(\boldsymbol x)$是凸函数当且仅当 \[\begin{align*} f(\boldsymbol y) - f(\boldsymbol x) \geq abla f(\boldsymbol x)^T \; (\boldsymbol y - \boldsymbol x), \ \forall \boldsymbol x, \boldsymbol y \in S. \end{align*}\]
若$f(\boldsymbol x)$是$\mathbb R^d$上的凸函数，$c \in \mathbb R$, 则$\{\boldsymbol x \in \mathbb R^d:\ f(\boldsymbol x) \leq c \}$ 和$\{\boldsymbol x \in \mathbb R^d:\ f(\boldsymbol x) < c \}$都是凸集。
设$f(x)$为定义在某区间$S$上的二阶可微的一元实函数，如果$f(x)$满足$f''(x) \geq 0, \forall x \in S$，则$f(x)$在$S$上为凸函数；如果$f(x)$满足$f''(x) > 0, \forall x \in S$，则$f(x)$在$S$上为严格凸函数。
设$f(\boldsymbol x)$是定义在开凸集$S \subset \mathbb R^d$上的二阶可微函数，若$ abla^2 f(\boldsymbol x), \boldsymbol x \in S$都是非负定阵，则$f(\boldsymbol x)$为凸函数；若$ abla^2 f(\boldsymbol x), \boldsymbol x \in S$都是正定阵，则$f(\boldsymbol x)$为严格凸函数。
设$f(\boldsymbol x)$是定义在凸集$S \subset \mathbb R^d$上的凸函数，则$f(\boldsymbol x)$在$S$的内核$\mathring{S}$ 上连续且满足局部Lipschitz条件，即$\forall \boldsymbol x \in \mathring{S}$, 存在常数$c$使得对$\boldsymbol x$的一个邻域内的$\boldsymbol y, \boldsymbol z$都有 $|f(\boldsymbol y) - f(\boldsymbol z)| \leq c \| \boldsymbol y - \boldsymbol z \|$。
设$f(x, y)$是凸集$S \subset X imes Y$上的凸函数，集合$B \subset Y$是一个凸集，集合$A=\{x \in X:\; \exists y \in B ext{使得} (x, y) \in S \}$为非空集，则$A$是凸集， $g(x) \stackrel{ riangle}{=} \inf_{y \in B} f(x, y)$是$A$上的凸函数。
对随机变量$X$，若$f(x)$是凸函数， $EX$和$E f(X)$存在，则$f(E X) \leq E f(X)$。这称为Jenson不等式。
设$f(\boldsymbol x)$为凸函数，$g(t), t \in \mathbb R$为单调增的凸函数，则$g(f(\boldsymbol x))$为凸函数。
设$A$为矩阵，$\boldsymbol b$为向量，$f(\boldsymbol x)$为凸函数，则$f(A \boldsymbol x + \boldsymbol b)$为凸函数。
如果$f(\boldsymbol x), g(\boldsymbol x)$为凸函数，$\alpha \geq 0, \beta \geq 0$, 则$\alpha f(\boldsymbol x) + \beta g(\boldsymbol x)$为凸函数。
如果$f(\boldsymbol x), g(\boldsymbol x)$为凸函数，则$\max(f(x), g(x))$为凸函数。
若$f(x, y)$定义于$x \in A$, $y \in B$， $A$是$\mathbb R^d$中的凸集，$B$是某足标集，若对任意$y \in B$， $f(x, y)$关于$x \in A$是凸函数，则$g(x) \stackrel{ riangle}{=}\sup_{y \in B} f(x, y)$是$A$上的凸函数；若对任意$y \in B$， $f(x, y)$关于$x \in A$是凹函数，则$g(x) \stackrel{ riangle}{=}\inf_{y \in B} f(x, y)$是$A$上的凹函数。
设$f_n(\boldsymbol x), n=1,2,\dots$都是凸函数且$\lim_{n o\infty} f_n(\boldsymbol x)$存在，则$f(\boldsymbol x) \stackrel{ riangle}{=} \lim_{n o\infty} f_n(\boldsymbol x)$是凸函数。
对数凸函数一定也是凸函数。
设$f(\boldsymbol x)$为凸函数，$g(t), t \in \mathbb R$为单调增的对数凸函数，则$g(f(\boldsymbol x))$是对数凸函数。
若$f(\boldsymbol x)$是对数凸函数，则$f(A \boldsymbol x + \boldsymbol b)$也是对数凸函数。
设$f(\boldsymbol x)$为对数凸函数，$\alpha>0$，则$f(\boldsymbol x)^\alpha$和$\alpha f(\boldsymbol x)$为对数凸函数。
设$f(\boldsymbol x), g(\boldsymbol x)$为对数凸函数，则$f(\boldsymbol x) + g(\boldsymbol x)$, $f(\boldsymbol x) g(\boldsymbol x)$ 和 $\max(f(\boldsymbol x), \; g(\boldsymbol x))$都是对数凸函数。
设$f_n(\boldsymbol x), n=1,2,\dots$都是对数凸函数且$\lim_{n o\infty} f_n(\boldsymbol x)$存在，则$f(\boldsymbol x) \stackrel{ riangle}{=} \lim_{n o\infty} f_n(\boldsymbol x)$是对数凸函数。

例35.6 设$\boldsymbol x \in \mathbb R^d$, $S$为$\mathbb R^d$的凸集，则$f(\boldsymbol x)= ext{dist}(\boldsymbol x, S)$是凸函数。

利用性质7可得此结论。

例35.7 $|x|$是凸函数。可以直接证明，或利用$|x|=\max(x, -x)$和性质12。

$x^+=\max(x, 0)$是凸函数。

$x^2$是凸函数。$\frac{d^2}{dx^2} x^2=2 > 0$。

例35.8 $f(x)=|x|^\gamma$是凸函数($\gamma \geq 1$)。首先, $g(x)=x^\gamma, x \in [0, \infty)$ 满足$g'(x)=\gamma x^{\gamma-1} \geq 0$, $g''(x)=\gamma (\gamma - 1) x^{\gamma-2} \geq 0$，所以$g(x)$在$[0, \infty)$上是单调增凸函数，而$|x|$是凸函数，所以$f(x)=g(|x|)$是凸函数。

例35.9 对线性函数$f(\boldsymbol x)=\boldsymbol a^T \boldsymbol x + b, \boldsymbol x \in \mathbb R^n$，其中$\boldsymbol a \in \mathbb R^d, b \in \mathbb R$, 有$ abla f(\boldsymbol x)=\boldsymbol a$, $ abla^2 f(\boldsymbol x)=0$， $f(\boldsymbol x)$是凸函数，且(35.9)中的等式成立。

例35.10 对$f(\boldsymbol x)=\frac12 \boldsymbol x^T A \boldsymbol x + \boldsymbol b^T \boldsymbol x + c, \boldsymbol x \in \mathbb R^n$, 其中$A$为非负定阵，$\boldsymbol b \in \mathbb R^d, c \in \mathbb R$, 有$ abla f(x)=A \boldsymbol x + \boldsymbol b$, $ abla^2 f(\boldsymbol x)=A$, 所以$f(\boldsymbol x)$是凸函数。当$A$是正定阵时， $f(\boldsymbol x)$是严格凸函数。

例35.11 欧式模$f(\boldsymbol x)=\| \boldsymbol x \|=\sqrt{\boldsymbol x^T \boldsymbol x}$是凸函数。

事实上，当$\boldsymbol x eq \boldsymbol 0$时$ abla f(\boldsymbol x)=\| \boldsymbol x \|^{-1} \boldsymbol x$, $ abla^2 f(\boldsymbol x)=\| \boldsymbol x \|^{-3}\left( \| \boldsymbol x \|^{2} I_d - \boldsymbol x \boldsymbol x^T \right)$, 其中$I_d$为$d$阶单位阵。易见$ abla^2 f(\boldsymbol x)$是非负定阵，但不是正定阵。进一步地，所有的范数（模）都是凸函数，见例35.5。

例35.12 设$\boldsymbol z_j, j=1,\dots,n$是$\mathbb R^d$的$n$个点。定义 \[\begin{aligned} f(\boldsymbol x)=\log \left[ \sum_{j=1}^n \exp(\boldsymbol z_j^T \boldsymbol x) \right], \end{aligned}\] 由于$\boldsymbol z_j^T \boldsymbol x$是凸函数，所以$\exp(\boldsymbol z_j^T \boldsymbol x)$是对数凸函数，由性质19可知$\sum_{j=1}^n \exp(\boldsymbol z_j^T \boldsymbol x)$是对数凸函数，即$f(\boldsymbol x)$是凸函数。

凸函数在最优化问题中有重要作用，原因是, 若$f(\boldsymbol x)$是凸集$S \subset \mathbb R^d$上的凸函数, 那么：

当$f(\boldsymbol x)$有一个局部极小值点$\boldsymbol x^*$时，这个极小值点也是全局最小值点，但不一定是唯一的全局最小值点，这时集合$\{ \boldsymbol x \in S : \ f(\boldsymbol x)=f(\boldsymbol x^*) \}$是一个凸集。
如果$\boldsymbol x^*$是$f(\boldsymbol x)$的一个稳定点，则$\boldsymbol x^*$是$f(\boldsymbol x)$的一个全局最小值点。
如果$f(\boldsymbol x)$是严格凸函数而且全局最小值点存在，这个全局最小值点是唯一的。

对于约束优化问题(35.1), 如果等式约束$c_i, i=1,\dots,p$都是线性函数，不等式约束$c_i, i=p+1, \dots, p+q$都是凸函数，目标函数$f(\boldsymbol x)$是凸函数，则称(35.1)为凸规划问题或凸优化问题。凸规划问题的可行域$D$是凸集(因为凸集的交集是凸集和凸函数性质4)，其局部极小值点一定是全局最小值点。

设$f(\boldsymbol x)$的定义域$\mathcal A$为$\mathbb R^d$中的开集。如果$\boldsymbol x^*$使得$ abla f(\boldsymbol x^*)=0$，称$\boldsymbol x^*$为$f(\cdot)$的一个稳定点。无约束极值点的必要条件和充分条件是数学分析中熟知的结论，这里仅罗列这些结论备查。

定理35.4 (一阶必要条件) 如果$f(\boldsymbol x), \boldsymbol x \in \mathcal A$有一阶连续偏导数， $\boldsymbol x^* \in \mathcal A$是$f(\cdot)$的一个局部极小值点，则$\boldsymbol x^*$是$f(\cdot)$的稳定点： \[\begin{align} abla f(\boldsymbol x^*)=\boldsymbol 0 . \end{align}\]

定理35.5 (二阶必要条件) 如果$f(\boldsymbol x), \boldsymbol x \in \mathcal A$有二阶连续偏导数， $\boldsymbol x^* \in \mathcal A$是$f(\cdot)$的一个局部极小值点，则$\boldsymbol x^*$是$f(\cdot)$的稳定点，且海色阵$ abla^2 f(\boldsymbol x^*)$为非负定阵。

定理35.6 (二阶充分条件) 如果$f(\boldsymbol x), \boldsymbol x \in \mathcal A$有二阶连续偏导数， $\boldsymbol x^* \in \mathcal A$是$f(\cdot)$的一个稳定点，且海色阵$ abla^2 f(\boldsymbol x^*)$为正定阵，则$\boldsymbol x^*$是$f(\cdot)$的局部严格极小值点。

稳定点不一定是极值点。如果$\boldsymbol x^*$是稳定点但是$ abla^2 f(\boldsymbol x^*)$同时有正特征值和负特征值，则$\boldsymbol x^*$一定不是$f(\cdot)$的极值点；如果$\boldsymbol x^*$是稳定点而$ abla^2 f(\boldsymbol x^*)$非负定但不正定，这时$\boldsymbol x^*$可能是$f(\cdot)$的极值点，也可能不是。

当所有$ abla^2 f(\boldsymbol x)$都是非负定（也称半正定）矩阵时， $f(\boldsymbol x)$是凸函数；当所有$ abla^2 f(\boldsymbol x)$都是正定矩阵时， $f(\boldsymbol x)$是严格凸函数。由凸函数的性质可得如下结论。

定理35.7 (全局最小值点的二阶充分条件) 如果$f(\boldsymbol x), \boldsymbol x \in \mathcal A$有二阶连续偏导数，所有$ abla^2 f(\boldsymbol x)$都是非负定阵， $\boldsymbol x^* \in \mathcal A$是$f(\cdot)$的一个稳定点，则$\boldsymbol x^*$是$f(\cdot)$的全局最小值点; 如果进一步设$ abla^2 f(\boldsymbol x^*)$是正定阵，则稳定点$\boldsymbol x^*$是全局严格最小值点。

定义35.6 (方向导数) 对向量$\boldsymbol v \in \mathbb R^d$, 若$\| \boldsymbol \|=1$，定义一元函数 \[\begin{aligned} h(\alpha)=f\left(\boldsymbol x + \alpha \boldsymbol v \right), \ \alpha \geq 0, \end{aligned}\] 如果$h(\alpha)$在$\alpha=0$的右导数存在，则称其为函数$f(\boldsymbol x)$在点$\boldsymbol x$沿方向$\boldsymbol v$的方向导数，记为$\frac{\partial f(\boldsymbol x)}{\partial \boldsymbol v}$；类似可定义二阶方向导数$\frac{\partial^2 f(\boldsymbol x)}{\partial \boldsymbol v^2}$。

如果$f(\boldsymbol x)$有一阶连续偏导数， $\| \boldsymbol v \|=1$, 则$\frac{\partial f(\boldsymbol x)}{\partial \boldsymbol v}=\boldsymbol v^T abla f(\boldsymbol x)$。如果$f(\boldsymbol x)$有二阶连续偏导数， $\| \boldsymbol v \|=1$, 则$\frac{\partial^2 f(\boldsymbol x)}{\partial \boldsymbol v^2}=\boldsymbol v^T abla^2 f(\boldsymbol x) \boldsymbol v$。

求无约束极值通常使用迭代法。设迭代中得到了一个近似极小值点$\boldsymbol x^{(t)}$，如果$ abla f(\boldsymbol x) eq \boldsymbol 0$，则从$\boldsymbol x^{(t)}$出发沿$- abla f(\boldsymbol x)$方向前进可以使函数值下降。而且，对任意非零向量$\boldsymbol v \in \mathbb R^d$, 只要$\boldsymbol v^T abla f(\boldsymbol x) < 0$，则$\frac{\partial f(\boldsymbol x)}{\partial \boldsymbol v} < 0$, 从$\boldsymbol x^{(t)}$出发沿$\boldsymbol v$方向前进也可以使函数值下降，称这样的方向$\boldsymbol v$为下降方向。

例35.13 考虑$d$元二次多项式 \[ f(\boldsymbol x)=\frac{1}{2} \boldsymbol x^T A \boldsymbol x + \boldsymbol b^T \boldsymbol x + c , \ \boldsymbol x \in \mathbb R^d . \] 设$A$为$d imes d$正定阵， $\boldsymbol b \in \mathbb R^d$， $c \in \mathbb R$。求$f(\boldsymbol x)$的最小值点。

这时， \[ abla f(\boldsymbol x)=A \boldsymbol x + \boldsymbol b, \quad abla^2 f(\boldsymbol x)=A, \] 求解$ abla f(\boldsymbol x)=0$可得 \[ \boldsymbol x_*=- A^{-1} \boldsymbol b . \] 由定理35.7， $\boldsymbol x_*$是$f(\boldsymbol x)$的全局严格最小值点。

※※※※※

例35.14 设$\boldsymbol Y$为$n imes 1$向量, $X$为$n imes p$矩阵($n > p$)， $\boldsymbol\beta$为$p imes 1$向量。求函数 \[\begin{align} Q(\boldsymbol\beta)=\| \boldsymbol Y - X \boldsymbol\beta \|^2 \end{align}\] 的极小值点的问题称为线性最小二乘问题。

易见 \[\begin{align} abla Q(\boldsymbol\beta)=& -2 X^T \boldsymbol Y + 2 X^T X \boldsymbol\beta, \\ abla^2 Q(\boldsymbol\beta)=& 2 X^T X, \end{align}\] 当$X$列满秩时$X^T X$为正定矩阵，这时稳定点$\hat{\boldsymbol\beta}=(X^T X)^{-1} X \boldsymbol Y$是$Q(\boldsymbol\beta)$全局严格最小值点。

如果$X$不满秩，因为$X^T X$是非负定矩阵，所以$Q(\boldsymbol\beta)$是凸函数，可以证明$Q(\boldsymbol\beta)$存在无穷多个稳定点，由定理35.7可知这些稳定点都是全局最小值点。

※※※※※

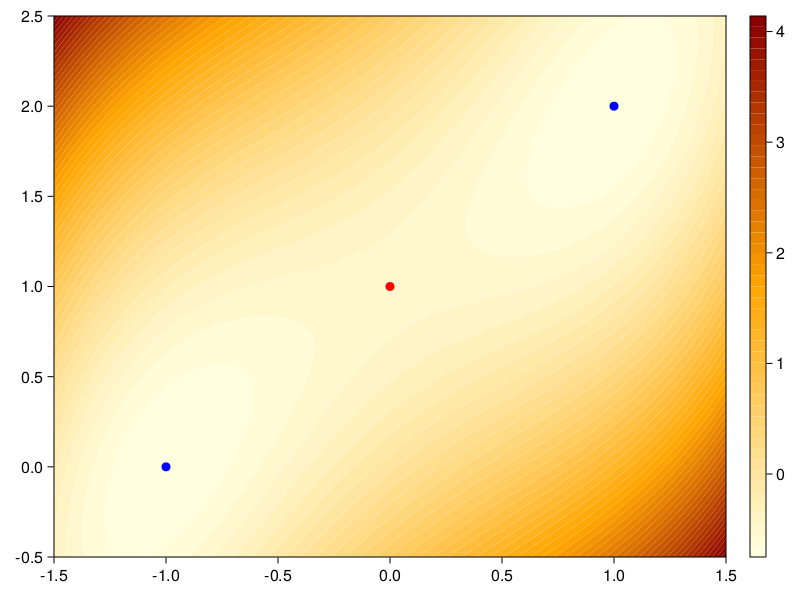
例35.15 求 \[\begin{aligned} \min f(\boldsymbol x)=\frac14 x_1^4 + \frac12 x_2^2 - x_1 x_2 + x_1 - x_2, \ \boldsymbol x \in \mathbb R^2 . \end{aligned}\]

易见 \[\begin{aligned} abla f(\boldsymbol x)=& \left(\begin{array}{cc} x_1^3 - x_2 + 1 \\ x_2 - x_1 - 1 \end{array}\right), \quad abla^2 f(\boldsymbol x)=\left(\begin{array}{cc} 3 x_1^2 & -1 \\ -1 & 1 \end{array}\right), \end{aligned}\] 令$ abla f(\boldsymbol x)=0$得到三个稳定点$(-1, 0), (1, 2), (0, 1)$。计算这三个点处的海色阵得 \[\begin{aligned} abla^2 f(-1,0)=& abla^2 f(1,2)=\left(\begin{array}{cc} 3 & -1 \\ -1 & 1 \end{array}\right), \quad abla^2 f(0,1)=\left(\begin{array}{cc} 0 & -1 \\ -1 & 1 \end{array}\right), \end{aligned}\] 前两个稳定点海色阵的特征值为$2 \pm \sqrt{2} > 0$，是正定阵，所以$(-1,0)$和$(1,2)$是$f(\cdot)$的极小值点，$f(-1, 0)=f(1,2)=-\frac34$，这两个点都是全局最小值点；稳定点$(0,1)$处的海色阵的特征值为$\frac12(1 \pm \sqrt{5})$，一正一负，所以$(0,1)$不是极小值点，且$f(0,1)=-\frac12$。

用Julia语言作函数的等高线图，标出三个稳定点：

※※※※※

与无约束最优化问题不同，约束极值点一般不满足梯度向量为零的条件，这是因为约束极值经常在可行域的边界达到，这时在极值点处如果不考虑约束条件，函数值仍可下降，所以约束极值点处的梯度不需要等于零向量。

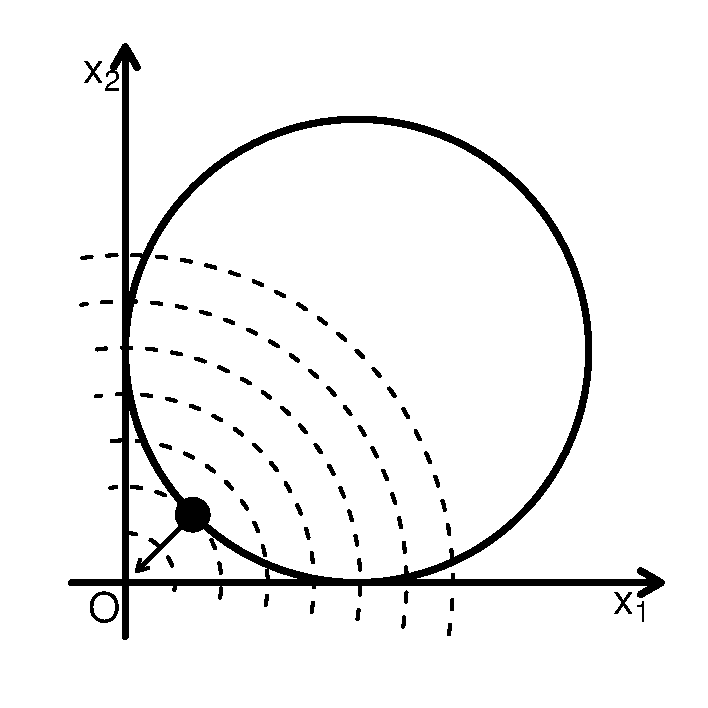
$例35.16图形。虚线为$f(\boldsymbol x)$的等值线，箭头是约束最小值点的负梯度方向$

图35.1: 例35.16图形。虚线为$f(\boldsymbol x)$的等值线，箭头是约束最小值点的负梯度方向

例35.16 考虑如下约束优化问题 \[\begin{align} \begin{cases} \mathop{ ext{argmin}} f(\boldsymbol x)=x_1^2 + x_2^2, \ ext{s.t.} \\ (x_1 - 1)^2 + (x_2 - 1)^2 \leq 1, \end{cases} \end{align}\] 可行域$D$是以$(1,1)^T$为圆心的半径等于1的圆面。容易看出约束最小值在$f(\boldsymbol x)$ 的等值线与$D$外切的点$\boldsymbol x^*=\left(1-\frac{\sqrt{2}}{2}, 1-\frac{\sqrt{2}}{2} \right)^T$处达到 (见图35.1)，这时$ abla f(\boldsymbol x^*)=(2-\sqrt{2}, 2-\sqrt{2})^T eq \boldsymbol 0$，沿着其反方向$(-1,-1)^T$搜索仍可使函数值下降，但会离开可行域。

在仅有等式约束的情形，如下的拉格朗日乘子法给出了约束极值点的必要条件。

定理35.8 考虑约束最优化问题 \[\begin{align} \begin{cases} & \mathop{ ext{argmin}}\limits_{\boldsymbol x \in \mathbb R^d } f(\boldsymbol x), \ ext{s.t.} \\ & c_i(\boldsymbol x)=0, \ i=1,\dots,p \\ \end{cases} ag{35.10} \end{align}\] 设$f(\cdot), c_i(\cdot)$在$\mathbb R^d$存在一阶连续偏导数，定义拉格朗日函数 \[\begin{align} L(\boldsymbol x, \boldsymbol\lambda)=f(\boldsymbol x) + \sum_{i=1}^p \lambda_i c_i(\boldsymbol x), ag{35.11} \end{align}\] 其中$\boldsymbol\lambda=(\lambda_1, \dots, \lambda_p)^T$，若$\boldsymbol x^*$是(35.10)的一个约束局部极小值点，则必存在$\boldsymbol\lambda^*$使得$(\boldsymbol x^*, \boldsymbol\lambda^*)$ 为$L(\boldsymbol x, \boldsymbol\lambda)$的稳定点, 即 \[\begin{align} & abla f(\boldsymbol x^*) + \sum_{i=1}^p \lambda_i^* abla c_i(\boldsymbol x^*)=0, ag{35.12}\\ & c_i(\boldsymbol x^*)=0, \ i=1,2,\dots,p. ag{35.13} \end{align}\]

条件(35.12)说明在约束局部极小值点，目标函数的梯度是各个约束的梯度的线性组合。这个定理将求等式约束的约束优化问题，转化成了关于拉格朗日函数$L(\boldsymbol x, \boldsymbol \lambda)$的无约束优化问题。

考虑如(35.1)那样的一般约束最优化问题。设可行域$D$为非空集。关于不等式约束$c_i, i=p+1, \dots, p+q$，对$\boldsymbol x \in D$，如果$c_i(\boldsymbol x)=0$，称$c_i$在$\boldsymbol x$处是起作用的，否则称$c_i$在$\boldsymbol x$处是不起作用的。实际上，假设$f, c_i$都连续，如果$\boldsymbol x^*$是一个约束局部极小值点，则去掉$\boldsymbol x^*$处不起作用的约束得到的新优化问题也以$\boldsymbol x^*$为一个约束局部极小值点。起作用的和不起作用的不等式约束的下标集合是随$\boldsymbol x$而变的，在本书中，为记号简单起见，设$c_i, i=p+1, \dots, p+r$($0 \leq r \leq q$)是起作用的不等式约束， $c_i, i=p+r+1, \dots, p+q$是不起作用的不等式约束，对实际问题则应使用两个随$\boldsymbol x$而变化的下标集合或每次重新排列约束次序。

由于可行域形状可能是多种多样的，需要特别地定义可行方向的概念。

定义35.7 (可行方向) 设$\boldsymbol x$是问题(35.1)的可行点，如果有$\boldsymbol d \in \mathbb R^d$，$\| \boldsymbol d \|=1$, 以及序列$\boldsymbol d^{(k)} \in \mathbb R^d$, $\| \boldsymbol d^{(k)} \|=1$, 和$\alpha_k > 0$，使得$\boldsymbol x^{(k)}=\boldsymbol x + \alpha_k \boldsymbol d^{(k)} \in D$, 且$\lim_{k o\infty} \boldsymbol x^{(k)}=\boldsymbol x$， $\lim_{k o\infty} \boldsymbol d^{(k)} o \boldsymbol d$, 则称$\boldsymbol d$是问题(35.1)在$\boldsymbol x$处的一个可行方向，记$\boldsymbol x$处所有可行方向的集合为$\mathscr F(\boldsymbol x)$。可行方向也称为序列可行方向。如果$\boldsymbol d \in \mathscr F(\boldsymbol x)$满足$\boldsymbol d^T abla f(\boldsymbol x) < 0$，称$\boldsymbol d$是$\boldsymbol x$处的一个可行下降方向。

另一种可行方向定义比较简单。

定义35.8 (线性化可行方向) 设$\boldsymbol x$是问题(35.1)的可行点， \[\begin{aligned} \mathscr L(\boldsymbol x) \stackrel{ riangle}{=} \big\{ \boldsymbol d \in \mathbb R^d:\ & \| \boldsymbol d \|=1,\ \boldsymbol d^T abla c_i(\boldsymbol x)=0, i=1,\dots, p; onumber\\ & \boldsymbol d^T abla c_i(\boldsymbol x) \leq 0, i=p+1,\dots, p+r \big\} \end{aligned}\] 称为$\boldsymbol x$处的线性化可行方向集，其中的元素称为$\boldsymbol x$处的线性化可行方向。

注意线性化可行方向定义只对等式约束和起作用的不等式约束有要求，不关心不起作用的不等式约束。可以证明，序列可行方向一定是线性化可行方向，反之不然。在线性化可行方向定义中，要求$\boldsymbol d$与等式约束$c_i(\boldsymbol x)$的梯度正交，所以沿$\boldsymbol d$略微移动使得$c_i(\boldsymbol x)$既不增加也不减少，保持等式不变；要求$\boldsymbol d$与起作用的不等式约束$c_i(\boldsymbol x)$的梯度不能成锐角，所以沿$\boldsymbol d$略微移动不能使得$c_i(\boldsymbol x)$增加，所以可以保持不等式成立。

如果$\boldsymbol x^*$是问题(35.1)的一个约束局部极小值点，则$\boldsymbol x^*$处没有可行下降方向，否则在$\boldsymbol x^*$附近可以找到函数值比$f(\boldsymbol x^*)$更小的可行点。另一方面，如果可行点$\boldsymbol x^*$处所有可行方向$\boldsymbol d \in \mathscr{F}(\boldsymbol x^*)$ 都是上升方向(即$\boldsymbol d^T abla f(\boldsymbol x)>0$)，则$\boldsymbol x^*$是一个约束严格局部极小值点。

鉴于可行方向集难以确定，以下的定理给出了约束极值点的一个比较容易验证的必要条件。

定理35.9 (Karush-Kuhn-Tucker) 对约束最优化问题(35.1)，假定目标函数$f(\boldsymbol x)$和约束函数$c_i(\boldsymbol x)$在$\mathbb R^d$有一阶连续偏导数， $\boldsymbol x^*$是一个约束局部极小值点，如果$c_i, i=1,\dots,p+r$都是线性函数，或者$\{ abla c_i(\boldsymbol x^*), i=1, \dots, p+r \}$ 构成线性无关向量组，则必存在常数$\lambda_1^*, \dots, \lambda_{p+q}^*$, 使得 \[\begin{align} & abla f(\boldsymbol x^*) + \sum_{i=1}^{p+q} \lambda_i^* abla c_i(\boldsymbol x^*)=0, ag{35.14}\\ & \lambda_i^* \geq 0, \ i=p+1, \dots, p+q, \\ & \lambda_i^* c_i(\boldsymbol x^*)=0, \ i=p+1,\dots, p+q. ag{35.15} \end{align}\]

对问题(35.1)仍可定义拉格朗日函数 \[\begin{aligned} L(\boldsymbol x, \boldsymbol\lambda)=f(\boldsymbol x) - \sum_{i=1}^{p+q} \lambda_i c_i(\boldsymbol x), \end{aligned}\] 定理结论中的(35.15)表明$L(\boldsymbol x^*, \boldsymbol\lambda^*)=f(\boldsymbol x^*)$, (35.14)可以写成$ abla_{\boldsymbol x} L(\boldsymbol x^*, \boldsymbol\lambda^*)=0$, 其中$ abla_{\boldsymbol x} L(\boldsymbol x, \boldsymbol\lambda)$ 表示$L(\boldsymbol x, \boldsymbol\lambda)$的梯度向量中与分量$\boldsymbol x$对应的部分。

定理证明略去(见高立 (2014) §6.3, Lange (2013) §5.2)。 (35.14)–(35.15)称为KKT条件或KT条件，迭代时满足KKT条件点$\boldsymbol x^*$称为KKT点, 对应的$\boldsymbol\lambda^*$称为拉格朗日乘子， $(\boldsymbol x^*, \boldsymbol\lambda^*)$称为KKT对。 KKT点类似于无约束优化问题中的稳定点，很多基于导数的算法在达到KKT点后就不能再继续搜索。

注意(35.15)保证了不起作用的不等式约束对应的乘子$\lambda_i^*=0, i=p+r+1, \dots, p+q$。这样，我们把KKT对$(\boldsymbol x^*, \boldsymbol\lambda^*)$ 处的约束条件$c_i(\boldsymbol x^*), i=1,\dots, p+q$和相应的拉格朗日乘子$\boldsymbol\lambda^*$分为四个部分:

$c_i(\boldsymbol x^*)=0$, $\lambda_i^*$可取正、负、零, $i=1,\dots,p$;
$c_i(\boldsymbol x^*)=0$, $\lambda_i^* > 0$, $i=p+1,\dots,p+r'$($r'\leq r$);
$c_i(\boldsymbol x^*)=0$, $\lambda_i^*=0$, $i=p+r'+1,\dots,p+r$;
$c_i(\boldsymbol x^*)<0$, $\lambda_i^*=0$, $i=p+r+1,\dots,p+q$。

其中，第一部分对应于等式约束，第二、第三部分对应于起作用的不等式约束，第四部分对应于不起作用的不等式约束。注意，这里为了记号简单起见用序号分开了这四部分，实际上第二、三、四部分的组成下标可以是$\{p+1, \dots, p+q \}$的任意分组。把(35.14)写成 \[\begin{aligned} abla f(\boldsymbol x^*)=-\sum_{i=1}^{p+r'} \lambda_i^* abla c_i(\boldsymbol x^*), \end{aligned}\] 对线性化可行方向$\boldsymbol d \in \mathscr L(\boldsymbol x^*)$, 有 \[\begin{aligned} \boldsymbol d^T abla f(\boldsymbol x^*)=-\sum_{i=1}^{p} \lambda_i^* \boldsymbol d^T abla c_i(\boldsymbol x^*) - \sum_{i=p+1}^{p+r'} \lambda_i^* \boldsymbol d^T abla c_i(\boldsymbol x^*) \geq 0, \end{aligned}\] 所以在KKT点没有线性化可行下降方向; 没有线性化可行下降方向是约束局部极小值点的必要条件，但不是充分条件。如果某个点$\boldsymbol x^*$处所有的可行方向$\boldsymbol d \in \mathscr F(\boldsymbol x^*)$都是严格上升方向，即$\boldsymbol d^T abla f(\boldsymbol x^*) > 0$，则$\boldsymbol x^*$是约束局部极小值点。如果存在与$ abla f(\boldsymbol x^*)$正交的可行方向，就需要进一步的信息来判断$\boldsymbol x^*$是不是约束极小值点。

在KKT对$(\boldsymbol x^*, \boldsymbol\lambda^*)$处定义 \[\begin{aligned} \mathscr L_1(\boldsymbol x^*, \boldsymbol \lambda^*) \stackrel{ riangle}{=} \big\{ \boldsymbol d \in \mathbb R^d: & \ \| \boldsymbol d \|=1, \boldsymbol d^T abla c_i(\boldsymbol x^*)=0, \ i=1,\dots, p+r'; onumber\\ & \boldsymbol d^T abla c_i(\boldsymbol x^*) \leq 0, i=p+r'+1, \dots, p+r \big\}, \end{aligned}\] 显然$\mathscr L_1(\boldsymbol x^*, \boldsymbol\lambda^*) \subset \mathscr L(\boldsymbol x^*)$, 且对$\boldsymbol d \in \mathscr L_1(\boldsymbol x^*, \boldsymbol\lambda^*)$有 \[\begin{aligned} \boldsymbol d^T abla f(\boldsymbol x^*)=& -\sum_{i=1}^{p+r'} \lambda_i^* \boldsymbol d^T abla c_i(\boldsymbol x^*)=0, \end{aligned}\] 即$\mathscr L_1(\boldsymbol x^*, \boldsymbol\lambda^*)$是$\mathscr L(\boldsymbol x^*)$中与梯度$ abla f(\boldsymbol x^*)$正交的方向。因为这样的方向可能存在，判断极小值点可能还需要二阶偏导数条件。这个问题的理由与一元函数导数等于零的点不一定是极值点的理由类似。

定理35.10 (二阶必要条件) 在定理35.9的条件下，进一步设在$\boldsymbol x^*$的一个邻域内$f$与各$c_i$有二阶连续偏导数，则有 \[\begin{align} \boldsymbol d^T abla_{\boldsymbol x \boldsymbol x}^2 L(\boldsymbol x^*, \boldsymbol \lambda^*) \boldsymbol d \geq 0, \ \forall \boldsymbol d \in \mathscr L_1(\boldsymbol x^*, \boldsymbol\lambda^*). ag{35.16} \end{align}\]

定理35.10给出了约束极小值点处拉格朗日函数关于$\boldsymbol x$的海色阵的必要条件，类似于无约束情形下要求目标函数海色阵非负定， (35.16)针对方向$\boldsymbol d \in \mathscr L_1(\boldsymbol x^*, \boldsymbol\lambda^*)$ 要求$ abla_{\boldsymbol x \boldsymbol x}^2 L(\boldsymbol x^*, \boldsymbol \lambda^*)$非负定。 $\mathscr L_1(\boldsymbol x^*, \boldsymbol\lambda^*)$ 是$\mathscr L(\boldsymbol x^*)$中与梯度$ abla f(\boldsymbol x^*)$正交的方向，为了$\boldsymbol x^*$是局部最小值点，对这样的方向需要加二阶导数条件，因为在这样的方向上变化仅从一阶导数看不出会不会下降。

定理35.11 (二阶充分条件) 对约束最优化问题(35.1)，假定目标函数$f$和各约束函数$c_i$在$\boldsymbol x^*$的邻域内有二阶连续偏导数，若($\boldsymbol x^*, \boldsymbol\lambda^*$)是KKT对，且 \[\begin{aligned} \boldsymbol d^T abla_{\boldsymbol x \boldsymbol x}^2 L(\boldsymbol x^*, \boldsymbol\lambda^*) \boldsymbol d > 0, \ \forall \boldsymbol d \in \mathscr L_1(\boldsymbol x^*, \boldsymbol\lambda^*), \end{aligned}\] 则$\boldsymbol x^*$是问题(35.1)的一个严格局部极小值点。

如果在KKT对$(\boldsymbol x^*, \boldsymbol\lambda^*)$处的$\mathscr L_1(\boldsymbol x^*, \boldsymbol\lambda^*)$为空集, 定理35.11结论成立。

定理35.10和定理35.11的证明参见高立 (2014) §6.4。

例35.17 利用Karush-Kuhn-Tucker定理可以证明如下不等式： \[\begin{aligned} \frac{1}{4} (x_1^2 + x_2^2) \leq e^{x_1 + x_2 - 2}, \ x_1 \geq 0, x_2 \geq 0. \end{aligned}\]

只要证明$f(\boldsymbol x)=-(x_1^2 + x_2^2) e^{-x_1 - x_2}$的最小值是$-4 e^{-2}$。取$p=0$, $q=2$, 约束函数$c_1(\boldsymbol x)=-x_1$, $c_2(\boldsymbol x)=-x_2$, 约束函数都是线性函数，极小值点应该满足条件 \[\begin{aligned} & e^{-x_1 - x_2} \left(\begin{array}{c} -2 x_1 + x_1^2 + x_2^2 \\ -2 x_2 + x_1^2 + x_2^2 \end{array}\right) + \lambda_1 \left(\begin{array}{c} -1 \\ 0 \end{array} \right) + \lambda_2 \left(\begin{array}{c} 0 \\ -1 \end{array}\right)=0, \\ & \lambda_1 \geq 0, \ \lambda_2 \geq 0, \\ & -\lambda_1 x_1=0, \ -\lambda_1 x_2=0. \end{aligned}\] 解集为$\{ (0, 0), (1, 1), (0, 2), (2, 0) \}$, 对应的目标函数值分别为$0$, $-2e^{-2}$, $-4 e^{-2}$, $-4 e^{-2}$。易见$\lim_{\| \boldsymbol x \| o\infty} f(\boldsymbol x)=0 > -4 e^{-2}$, 所以目标函数$f(\boldsymbol x)$能达到最小值, 所以全局约束最小值点是$(0,2)$和$(2,0)$，最小值是$-4 e^{-2}$。

作为示例，用二阶条件来判断$\boldsymbol x^*=(2, 0)^T$是否局部极小值点。解出对应的拉格朗日乘子为$\boldsymbol\lambda^*=(0, 4 e^{-2})^T$, 两个约束条件中第二个起作用且对应的拉格朗日乘子为正，第一个不起作用，又$ abla c_1(\boldsymbol x^*)=(-1, 0)^T$, $ abla c_2(\boldsymbol x^*)=(0, -1)^T$, \[\begin{aligned} \mathscr L_1(\boldsymbol x^*, \boldsymbol\lambda^*)=\{ \boldsymbol d : \ \| \boldsymbol d \|=1, \boldsymbol d^T (-1,0)^T \leq 0, \boldsymbol d^T (0,-1)^T=0 \}=\{ (1, 0)^T \}, \end{aligned}\] 计算可得$(1,0) abla^2 L_{\boldsymbol x \boldsymbol x}(\boldsymbol x^*, \boldsymbol\lambda^*) (1,0)^T=2e^{-2} > 0$，所以$\boldsymbol x^*=(2,0)^T$是局部极小值点。

※※※※※

最优化和方程求根普遍使用迭代算法，从上一步的近似值$\boldsymbol x^{(t)}$通过迭代公式得到下一步的近似值$\boldsymbol x^{(t+1)}$。设$\lim_{t o\infty} \boldsymbol x^{(t)}=\boldsymbol x^*$，下面给出收敛速度的一些度量。

定义35.9 如果存在$r>0$和$c>0$使得 \[ \lim_{n o\infty} \frac{ \| \boldsymbol x^{(t+1)} - \boldsymbol x^* \|} { \| \boldsymbol x^{(t)} - \boldsymbol x^* \|^r}=c \] 称算法为$r$阶收敛，收敛常数为$c$。

定义35.10 令 \[\begin{align*} Q_1=\varlimsup_{t o\infty} \frac{ \| \boldsymbol x^{(t+1)} - \boldsymbol x^* \|}{ \| \boldsymbol x^{(t)} - \boldsymbol x^* \|}, \end{align*}\] 则$Q_1=0$时称算法超线性收敛, 当$0<Q_1<1$时称算法线性收敛, 当$Q_1=1$时称算法次线性收敛。

线性收敛是1阶收敛，收敛常数为$Q_1$。

定义35.11 令 \[\begin{align*} Q_2=\varlimsup_{t o\infty} \frac{ \| \boldsymbol x^{(t+1)} - \boldsymbol x^* \|}{ \| \boldsymbol x^{(t)} - \boldsymbol x^* \|^2}, \end{align*}\] 则$Q_2=0$时称算法超平方收敛, 当$0<Q_2<+\infty$时称算法平方收敛或二次收敛, 当$Q_2=+\infty$时称算法次平方收敛。

二次收敛即2阶收敛，收敛常数为$Q_2$。

最优化算法至少应该有线性收敛速度，否则收敛太慢，实际中无法使用。

实际的最优化问题不一定满足算法收敛的条件，而且往往难以预先判断是否能够收敛。所以，最优化算法对于何时停止迭代，通常使用目标函数值$f(\boldsymbol x^{(t)})$两次迭代之间的变化量 $|f(\boldsymbol x^{(t+1)}) - f(\boldsymbol x^{(t)})|$小于预定精度值、迭代近似点$\boldsymbol x^{(t)}$两次之间的变化量$\| \boldsymbol x^{(t+1)} - \boldsymbol x^{(t)} \|$小于预定精度值、梯度向量长度$\| abla f(\boldsymbol x^{(t)}) \|$小于预定精度值等作为停止法则，对于约束优化问题还要考虑对约束的符合程度。注意，按照这样的法则停止时并不能保证求解序列逼近了真实的全局或局部极小值点，迭代序列是否收敛到最优解依赖于问题与优化算法。

另外，为了保险起见，当迭代次数超出一个预定最大次数时也停止，但是这时给出算法失败的结果。

在统计计算问题中，目标函数$f(\boldsymbol x)$常常不能计算到很高精度，有时目标函数值甚至是由随机模拟方法计算得到的，这样，迭代停止法则不能选取过高的精度，否则算法可能在极值点附近不停跳跃而无法收敛。

可以对一元函数在指定区间求根。

函数进行一元函数优化求解。

函数可以进行多元函数无约束最优化，支持Nelder-Mead、BFGS、模拟退化等算法，也支持简单的区间约束问题求解。

求解最小二乘问题。

例35.18 例35.15的求解。

可以从初值出发用Nelder-Mead方法对目标函数求解无约束优化问题。

它找到了两个最小值点之一的$(-1, 0)$。

使用BFGS方法：

结果类似。

JuMP是Julia语言的一个最优化问题建模求解软件包，在不同后端计算软件支持下可以计算广泛的最优化问题。 Convex包也是一个功能强大的优化软件包。

Optim是一个纯粹用Julia语言编写的优化求解软件包，功能比较少，主要针对无约束优化问题。

例35.19 例35.15的求解。

用Optim包求解：

其中ores显示的结果为：

定理35.1（一阶必要条件）的证明：

已知$x^* \in (a, b)$，存在$\delta > 0$，使得当$0 < h < \delta$时 \[ f(x^* \pm h) \geq f(x^*) . \] 做泰勒展开得 \[ f(x^* \pm h)=f(x^*) \pm h f'(x^*) + o(h) \geq f(x^*), \] 即 \[ \pm h f'(x^*) + o(h) \geq 0, \] 于是 \[ o(h) \geq \pm h f'(x^*), \quad o(h) \geq h |f'(x^*)|, \] 取极限 \[ 0=\lim_{h \downarrow 0} \frac{o(h)}{h} \geq |f'(x^*)| \geq 0, \] 故$f'(x^*)=0$，得证。

※※※※※

定理35.2（二阶必要条件）的证明：

类似地作泰勒展开 \[ f(x^* \pm h)=f(x^*) \pm h f'(x^*) + \frac{1}{2} h^2 f''(x^*) + o(h^2) \geq f(x^*), \] 其中$f'(x^*)=0$，有 \[ \frac{1}{2} h^2 f''(x^*) + o(h^2) \geq 0, \] 从而 \[ \frac{1}{2} f''(x^*) + o(1) \geq 0, \ (h \downarrow 0), \] 令$h \downarrow 0$得$f''(x^*) \geq 0$。

※※※※※

定理35.3（二阶充分条件）的证明：

由 \[ f''(x^*)=\lim_{h o 0} \frac{f'(x^* + h) - f'(x^*)}{h}=\lim_{h o 0} \frac{f'(x^* + h)}{h} > 0, \] 存在$\delta > 0$使得$0 < |h| < \delta$时 $f'(x^* + h)$与$h$同号，因此函数$f(x)$在$(x^* - \delta, x^*)$为减函数，在$(x^*, x^* + \delta)$为增函数，所以$x^*$是局部极小值点。

※※※※※

习题1

设$\boldsymbol x=(x_1, x_2, \dots, x_n) \in \mathbb R^n$, $\boldsymbol y=(y_1, y_2, \dots, y_n) \in \mathbb R^n$，证明如下的Cauchy-Schwarz不等式: \[\begin{align*} \big|(\boldsymbol x, \boldsymbol y) \big| \leq \| \boldsymbol x \| \cdot \| \boldsymbol y \| \end{align*}\] 其中$(\boldsymbol x, \boldsymbol y)=\sum_{i=1}^n x_i y_i$, $\| \boldsymbol x \|=\sqrt{\sum_{i=1}^n x_i^2}$，不等式中等号成立当且仅当存在实数$a, b$使得$a \boldsymbol x + b \boldsymbol y=0$。

习题2

证明凸集性质1–10。

习题3

证明无约束和有约束的凸规划问题的局部最优解一定是全局最优解。

习题4

对例35.14, 证明当$X$不满秩时方程$X^T X \boldsymbol\beta=X^T Y$有无穷多解, 任一个解$\boldsymbol\beta^*$都是$Q(\boldsymbol\beta)$的全局最小值点。

习题5

在定理35.9条件下，如果$\{ abla c_i(\boldsymbol x^*), i=1, \dots, p+r \}$ 构成线性无关向量组，则$\boldsymbol\lambda^*$唯一。

习题6

对约束优化问题 \[\begin{align*} \begin{cases} & \mathop{ ext{argmin}} f(x_1, x_2) \stackrel{ riangle}{=} 4 x_1 - 3 x_2, \quad ext{s.t.} \\ & 4 - x_1 - x_2 \geq 0, \\ & x_2 + 7 \geq 0, \\ & -(x_1 - 3)^2 + x_2 + 1 \geq 0 \end{cases} \end{align*}\] 求其KKT点，并根据二阶条件判断KKT点是否最小值点。

习题7

设函数$f(\boldsymbol x)$定义在$\mathbb R^d$上，有一阶连续偏导数， $\boldsymbol v \in \mathbb R^d$, $\| \boldsymbol v \|=1$。令$h(\alpha)=f(\boldsymbol x + \alpha \boldsymbol v)$, $\alpha \geq 0$, 证明$h'(0)=\boldsymbol v^T abla f(\boldsymbol x)$。对一般的$\boldsymbol u \in \mathbb R^d$，若$\| \boldsymbol u \| > 0$，仍有 \[ \frac{d}{d \alpha} f(\boldsymbol x + \alpha \boldsymbol u)|_{\alpha=0}=\boldsymbol u^T abla f(\boldsymbol x) . \]

上一篇 : 电竞之都成都篇：手游之都做电竞的优势与劣势｜电竞世界

下一篇 : 如何评价智能优化算法的麻雀搜索算法？

联系我们

公司动态

35 最优化问题

习题1

习题2

习题3

习题4

习题5

习题6

习题7