几何优化方法介绍

时间：2024-05-26 09:41:00 浏览：次

几何优化(Geometry Optimization)是计算化学中的基础计算任务。当分子体系处于稳定构型时(势能面上极小值点)，各个原子核受到的力均为0，因此优化几何构型的思路是：从某个试探性的初始分子几何构型出发，让每个原子核都向受力减小的方向移动直至受力为0，实际计算中是受力小于收敛标准即可。

常用的方法有一次优化法和二次优化法，分别是利用一次导数和二次导数求极值的方法。

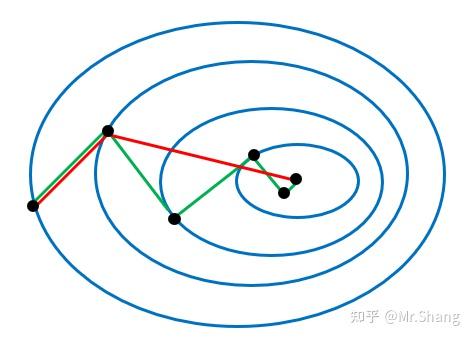
最速下降法通常采用线搜法寻找能量最小值点。势能U的负梯度方向为原子受力方向，对于处于某一构象的分子，沿受力方向移动能量逐渐降低，理论上可以找到该方向上的能量最小值点，再以此点为始点重新计算梯度，重复上述步骤即可找出函数的最小值点。线搜法相邻搜索方向相互正交。

优点：理论上一定可以找到能量函数的极小值

缺点：在接近收敛点是收敛速度很慢，甚至达不到收敛点

共轭梯度法的移动方向为新的负梯度方向与上一个搜索方向的线性组合，表达式如下：

$\\vec{v_{k}}=-\\vec{g_{k}}+γ_{k}\\vec{v_{k-1}}\\\\$ $\\gamma_{k}=\\frac{\\vec{g_{k}}\\cdot\\vec{g_{k}}}{\\vec{g_{k-1}}\\cdot\\vec{g_{k-1}}}\\\\$ $\\vec{v_{k}}$ 为第k步的搜索方向， ${\\gamma_{k}}$ 为线性组合系数， $\\vec{g_{k}}$ 为第k步负梯度方向。

优点：克服了最速下降法收敛慢的缺点，又避免了牛顿法需要存储与计算Hessian矩阵并求逆的缺点，可用于精确寻找最低能量构象

将多元函数 $f(X)$ 在 $x^{(k)}$ 处展开成Taylor级数，并取二阶近似，公式如下：

$f(X)\\approx f(x^{(k)})+\ abla f(x^{(k)})^{T}(x-x^{(k)})+\\frac{1}{2}(x-x^{(k)})^T\ abla^2f(x^{(k)})(x-x^{(k)})\\\\$ $\ abla f(x^{(k)})$ 为 $f(X)$ 在 $x^{(k)}$ 处的一阶偏导矩阵，称为Jacobi矩阵，记作 $J$ ； $\ abla^{2}f(x^{(k)})$ 为 $f(X)$ 在 $x^{(k)}$ 处的二阶偏导矩阵，称为Hessian矩阵，记作 $H$ 。

在几何优化中，多元函数 $f(X)$ 为势能 $U$ ，若体系包含 $N$ 个原子，势能 $U$ 是3N个变量的函数，故Hessian矩阵 $U^{''}(x^{(k)})$ 是 $3N\ imes3N$ 矩阵。

因为 $f^{'}(X)$ 在极小值处为0，所以对上式求导并等于0，可以得到下式：

$J+H_{}(x-x^{(k)})=0\\\\$ 若Hessian矩阵 $H$ 可逆(满秩)，可以得到牛顿法的迭代公式如下：

$x^{(k+1)}=x^{(k)}-H^{-1}J\\\\$ 牛顿法要求初始结构要尽可能较靠近极小点，越靠近极小点，这种方法效果越好。

缺点：（1）Hessian矩阵必须为正定矩阵(等价于特征值均为正)，否则会导致能量向较高处移动；（2）计算Hessian矩阵的逆矩阵时计算量很大

拟牛顿法的基本思想是用不包含二阶导数的矩阵近似牛顿法中Hessian矩阵的逆矩阵。

将 $f(X)$ 在 $x^{(k+1)}$ 处展开成Taylor级数，取二阶近似，如下：

$f(X)\\approx f(x^{(k+1)})+\ abla f(x^{(k+1)})^{T}(x-x^{(k+1)})+\\frac{1}{2}(x-x^{(k+1)})^T\ abla^2f(x^{(k+1)})(x-x^{(k+1)})\\\\$ 将 $x=x^{(k)}$ 代入 $f^{'}(X)$ 可得：