今天为各位讲解Jaya算法,Jaya算法提出时间比较晚,比较有趣的一点是Jaya算法的提出者与教学优化算法的提出者是同一位学者:R. Venkata Rao。
各位一定非常好奇为什么叫Jaya算法?该算法努力通过达到最优解来取得胜利,因此将其命名为 Jaya(Jaya是梵文,意思是胜利)。
相比于教学优化算法的两个阶段(即教师阶段与学习阶段),Jaya算法只有一个阶段,并具有无参数运行、求解速度快、不易陷入局部最优解等优点。
目录
▎Jaya算法更新解的策略
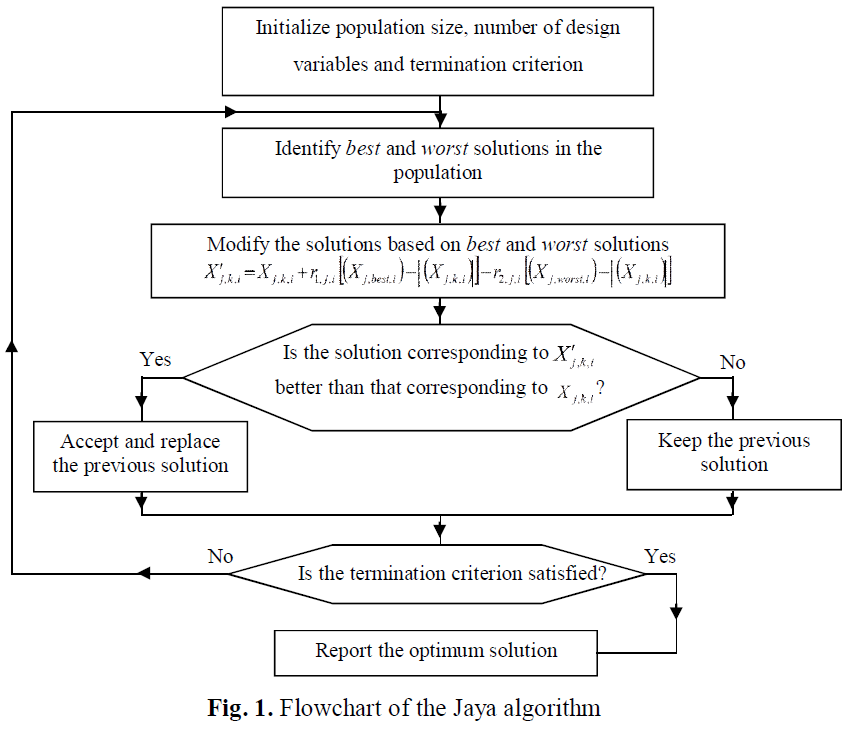
Jaya算法的基本思想是趋近最优解,远离最差解。因此,Jaya算法更新位置的公式如下:
其中是第i次迭代过程中第k个个体的第j个变量,
是第i次迭代过程中目标函数值最好个体的第j个变量,
是第i次迭代过程中目标函数值最差个体的第j个变量,
是
的绝对值,
和
是0~1之间的随机数。
是
更新后的值。
从上述公式可以看出,表现出是当前解向最好解靠拢的趋势,
表现出是当前解远离最差解的趋势。
▎Jaya算法流程图
▎Jaya算法实例验证
实例验证函数如下,目标是求解下述函数最小值:
目标函数Sphere函数代码如下:
function [f]= Sphere(x)
f= sum(x.^2);
end主函数代码如下:
%% JAYA algorithms
clc
clear all
close all
%% Problem Definition
pop = 1000; % Population size
var = 10; % Number of design variables
maxGen = 3000; % Maximum number of iterations
mini = -100*ones(1,var); % Lower Bound of Variables
maxi = 100*ones(1,var); % Upper Bound of Variables
objective = @Sphere; % Cost Function
%% initialize
[row,var] = size(mini);
x = zeros(pop,var);
fnew = zeros(pop,1);
f = zeros(pop,1);
fopt= zeros(pop,1);
xopt=zeros(1,var);
%% Generation and Initialize the positions
for i=1:var
x(:,i) = mini(i)+(maxi(i)-mini(i))*rand(pop,1);
end
for i=1:pop
f(i) = objective(x(i,:));
end
%% Main Loop
gen=1;
while(gen <= maxGen)
[row,col]=size(x);
[t,tindex]=min(f);
Best=x(tindex,:);
[w,windex]=max(f);
worst=x(windex,:);
xnew=zeros(row,col);
for i=1:row
for j=1:col
xnew(i,j)=(x(i,j))+rand*(Best(j)-abs(x(i,j))) - (worst(j)-abs(x(i,j))); %
end
end
for i=1:row
xnew(i,:) = max(min(xnew(i,:),maxi),mini);
fnew(i,:) = objective(xnew(i,:));
end
for i=1:pop
if(fnew(i)<f(i))
x(i,:) = xnew(i,:);
f(i) = fnew(i);
end
end
fnew = []; xnew = [];
[fopt(gen),ind] = min(f);
xopt(gen,:)= x(ind,:);
gen = gen+1;
disp(['Iteration No.=',num2str(gen), ', Best Cost=',num2str(min(f))])
end
%%
[val,ind] = min(fopt);
Fes = pop*ind;
disp(['Optimum value=',num2str(val,10)])
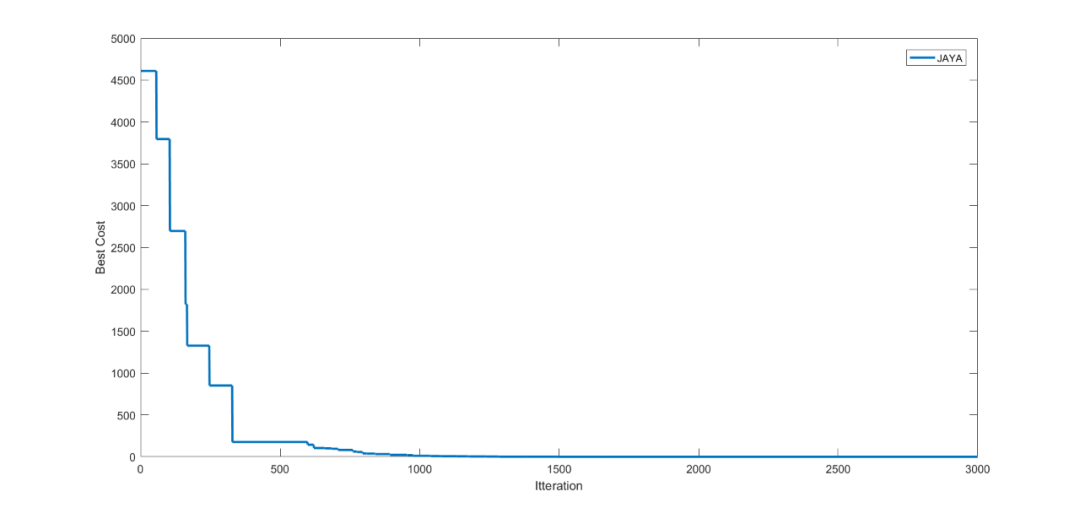
figure(1)
plot(fopt,'linewid',2)
xlabel('Itteration')
ylabel('Best Cost');
legend('JAYA')
disp(' ' )求解结果如下:

▎参考文献
[1]Rao R. Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems[J]. International Journal of Industrial Engineering Computations, 2016, 7(1): 19-34.
咱们下期再见
▎近期你可能错过了的好文章:
新书上架 | 《MATLAB智能优化算法:从写代码到算法思想》